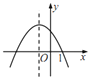题目内容
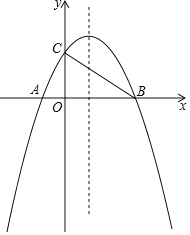
【题目】二次函数
图像如图，对称轴为直线
，则下列叙述正确的是（ ）
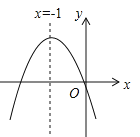
A.ac>0B.b2<4acC.b=2aD.a+b+c>0
【答案】C
【解析】
由抛物线开口方向得到a＜0，由图像与y轴的交点可知c<0，再根据抛物线的对称轴为直线x=-
=-1，得到b=2a，所以b＜0，2a-b=0；根据抛物线与x轴的交点个数得到b2-4ac＞0；根据自变量为1时，对应的函数值小于0得到a+b+c＜0．
解：∵抛物线开口向下，
∴a＜0，
∵c<0，
∴ac>0，故A错误；
∵抛物线与x轴有两个交点，
∴b2-4ac＞0，即b2>4ac，所以B错误；
∵抛物线的对称轴为直线x=-=-1，
∴b=2a，故C正确；
∵当x=1时，y＜0，
∴a+b+c＜0，所以D错误．
故选C．
【题目】现有
、
型两种客车，它们的载客量和租金如下表：
|
| |
载客量/（人/辆） |
|
|
租金/（元/辆） |
|
|
某学校计划在总费用
元的限额内，租用、型客车共5辆送九年级师生集体外出活动.
（Ⅰ）设租用型客车
辆（为非负整数），根据题意，用含的式子填写下表：
车辆数/辆 | 载客量 | 租金/元 | |
|
|
|
|
|
|
（Ⅱ）若九年级师生共有
人，请给出能完成此项任务的最节省费用的租车方案，并说明理由.
【题目】瑞安市曹村镇“八百年灯会”成为温州“申遗”的宝贵项目．某公司生产了一种纪念花灯，每件纪念花灯制造成本为18元．设销售单价x（元），每日销售量y（件）每日的利润w（元）．在试销过程中，每日销售量y（件）、每日的利润w（元）与销售单价x（元）之间存在一定的关系，其几组对应量如下表所示：
（元） | 19 | 20 | 21 | 30 |
（件） | 62 | 60 | 58 | 40 |
（1）根据表中数据的规律，分别写出毎日销售量y（件），每日的利润w（元）关于销售单价x（元）之间的函数表达式．（利润＝（销售单价﹣成本单价）×销售件数）．
（2）当销售单价为多少元时，公司每日能够获得最大利润？最大利润是多少？
（3）根据物价局规定，这种纪念品的销售单价不得高于32元，如果公司要获得每日不低于350元的利润，那么制造这种纪念花灯每日的最低制造成本需要多少元？