题目内容
【题目】如图,已知直线![]() 与
与![]() 轴、
轴、![]() 轴交与
轴交与![]() 、
、![]() 两点,抛物线
两点,抛物线![]() 经过点
经过点![]() 、
、![]() .
.
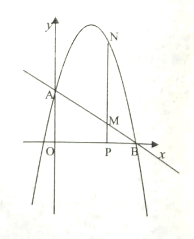

备用图
(1)求这个抛物线的解析式;
(2)点![]() 为线段
为线段![]() 上一个动点,过点
上一个动点,过点![]() 作垂直于
作垂直于![]() 轴的直线交抛物线于点
轴的直线交抛物线于点![]() ,交直线
,交直线![]() 于点
于点![]() .
.
①点![]() 是直线
是直线![]() 上方抛物线上一点,当
上方抛物线上一点,当![]() 相似时,求出点
相似时,求出点![]() 的坐标.
的坐标.
②若![]() ,求点
,求点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)①
;(2)①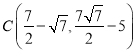 ,②
,②![]() .
.
【解析】
(1)利用一次函数图象上点的坐标特征可求出点A,B的坐标,由点A,B的坐标,利用待定系数法即可求出抛物线的解析式;
(2)①设点P的坐标为(x,0),则点N的坐标为(x,-x2+![]() x+2),点C的坐标为(
x+2),点C的坐标为(![]() -x,-x2+
-x,-x2+![]() x+2),点M的坐标为(-
x+2),点M的坐标为(-![]() x+2),进而可得出MN=-x2+4x,CN=|2x-
x+2),进而可得出MN=-x2+4x,CN=|2x-![]() |,由相似三角形的性质即可得出关于x的方程,解之即可得出x的值,进而可得出点C的坐标;
|,由相似三角形的性质即可得出关于x的方程,解之即可得出x的值,进而可得出点C的坐标;
②过点N作NE⊥AB于点E,设点P的坐标为(m,0),则PM=-![]() m+2,MN=-m2+4m,利用相似三角形的性质及特殊角的三角函数值可用含m的代数式表示出BM,ME,AE的长度,再利用勾股定理即可得出关于m的一元二次方程,解之取其正值即可得出结论.
m+2,MN=-m2+4m,利用相似三角形的性质及特殊角的三角函数值可用含m的代数式表示出BM,ME,AE的长度,再利用勾股定理即可得出关于m的一元二次方程,解之取其正值即可得出结论.
解:(1)当x=0时,y=-![]() x+2=2,
x+2=2,
∴点A的坐标为(0,2);
当y=0时,-![]() x+2=0,
x+2=0,
解得:x=4,
∴点B的坐标为(4,0).
将A(0,2),B(4,0)代入y=-x2+bx+c,得:![]() ,
,
解得:![]() ,
,
∴这个抛物线的解析式为y=-x2+![]() x+2.
x+2.
(2)①当△MNC∽△BPM相似时,如图1所示.
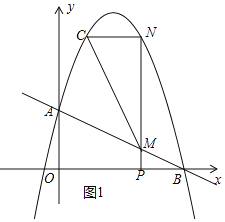
设点P的坐标为(x,0),则点N的坐标为(x,-x2+![]() x+2),点C的坐标为(
x+2),点C的坐标为(![]() -x,-x2+
-x,-x2+![]() x+2),点M的坐标为(x,-
x+2),点M的坐标为(x,-![]() x+2),
x+2),
∴MN=-x2+![]() x+2-(-
x+2-(-![]() x+2)=-x2+4x,CN=|x-(
x+2)=-x2+4x,CN=|x-(![]() -x)|=|2x-
-x)|=|2x-![]() |.
|.
∵△MNC∽△BPM,
∴![]() ,即
,即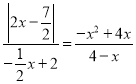 ,
,
解得:x1=![]() ,x2=-
,x2=-![]() (舍去),x3=1,x4=7(舍去),
(舍去),x3=1,x4=7(舍去),
∴![]() 或
或![]() ,
,
∴当△MNC∽△BPM时,点C的坐标为(![]() )或(
)或(![]() ).
).
②过点N作NE⊥AB于点E,如图2所示.
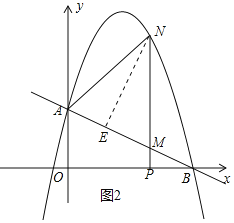
设点P的坐标为(m,0),则PM=-![]() m+2,MN=-m2+4m,
m+2,MN=-m2+4m,
∴BM=![]() PM=-
PM=-![]() m+2
m+2![]() ,ME=
,ME=![]() MN=
MN=![]() (-m2+4m),
(-m2+4m),
NE=2ME=![]() (-m2+4m),AE=tan30°×NE=
(-m2+4m),AE=tan30°×NE=![]() NE=
NE=![]() (-m2+4m),
(-m2+4m),
∴BM+ME+AE=AB,
即-![]() m+
m+![]() (-m2+4m)+
(-m2+4m)+![]() (-m2+4m)=
(-m2+4m)=![]() ,
,
整理得:(![]() )m2-(
)m2-(![]() )m=0,
)m=0,
解得:m1=0(舍去),m2=![]() ,
,
∴当∠NAB=60°时,点P的坐标为(![]() ,0),即
,0),即![]() .
.

 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案【题目】甲、乙两人“五一”放假期间去登盘山挂月峰,甲先开车沿小路开到了距离登山入口100米的地方后,开始以10米/分钟的登山上升速度徒步登山;甲开始徒步登山同时,乙直接从登山入口开始徒步登山,起初乙以15米/分钟的登山上升速度登山,两分钟后得知甲已经在半山腰,于是乙以甲登山上升速度的3倍提速.两人相约只登到距地面高度为300米的地方,设两人徒步登山时间为![]() (分钟)
(分钟)
(Ⅰ)根据题意,填写下表:
徒步登山时间/时间 | 2 | 3 | 4 | 5 | … |
甲距地面高度/米 | 120 | ______ | 140 | ______ | … |
乙距地面高度/米 | 30 | 60 | ______ | ______ | … |
(Ⅱ)请分别求出甲、乙两人徒步登山全程中,距地面的高度![]() (米)与登山时间
(米)与登山时间![]() (分)之间的函数关系式;
(分)之间的函数关系式;
(Ⅲ)登山多长时间时,甲、乙两人距地面的高度差为70米?