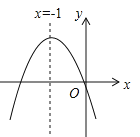ЬтФПФкШн
ЁОЬтФПЁПШ№АВЪаВмДхеђЁААЫАйФъЕЦЛсЁБГЩЮЊЮТжнЁАЩъвХЁБЕФБІЙѓЯюФПЃЎФГЙЋЫОЩњВњСЫвЛжжМЭФюЛЈЕЦЃЌУПМўМЭФюЛЈЕЦжЦдьГЩБОЮЊ18дЊЃЎЩшЯњЪлЕЅМлxЃЈдЊЃЉЃЌУПШеЯњЪлСПyЃЈМўЃЉУПШеЕФРћШѓwЃЈдЊЃЉЃЎдкЪдЯњЙ§ГЬжаЃЌУПШеЯњЪлСПyЃЈМўЃЉЁЂУПШеЕФРћШѓwЃЈдЊЃЉгыЯњЪлЕЅМлxЃЈдЊЃЉжЎМфДцдквЛЖЈЕФЙиЯЕЃЌЦфМИзщЖдгІСПШчЯТБэЫљЪОЃК
ЃЈдЊЃЉ | 19 | 20 | 21 | 30 |
ЃЈМўЃЉ | 62 | 60 | 58 | 40 |
ЃЈ1ЃЉИљОнБэжаЪ§ОнЕФЙцТЩЃЌЗжБ№аДГіАШеЯњЪлСПyЃЈМўЃЉЃЌУПШеЕФРћШѓwЃЈдЊЃЉЙигкЯњЪлЕЅМлxЃЈдЊЃЉжЎМфЕФКЏЪ§БэДяЪНЃЎЃЈРћШѓЃНЃЈЯњЪлЕЅМлЉГЩБОЕЅМлЃЉЁСЯњЪлМўЪ§ЃЉЃЎ
ЃЈ2ЃЉЕБЯњЪлЕЅМлЮЊЖрЩйдЊЪБЃЌЙЋЫОУПШеФмЙЛЛёЕУзюДѓРћШѓЃПзюДѓРћШѓЪЧЖрЩйЃП
ЃЈ3ЃЉИљОнЮяМлОжЙцЖЈЃЌетжжМЭФюЦЗЕФЯњЪлЕЅМлВЛЕУИпгк32дЊЃЌШчЙћЙЋЫОвЊЛёЕУУПШеВЛЕЭгк350дЊЕФРћШѓЃЌФЧУДжЦдьетжжМЭФюЛЈЕЦУПШеЕФзюЕЭжЦдьГЩБОашвЊЖрЩйдЊЃП
ЁОД№АИЁПЃЈ1ЃЉyЃНЉ2x+100ЃЌwЃНЉ2x2+136xЉ1800ЃЛЃЈ2ЃЉЕБЯњЪлЕЅМлЮЊ34дЊЪБЃЌУПШеФмЛёЕУзюДѓРћШѓЃЌзюДѓРћШѓЪЧ512дЊЃЛЃЈ3ЃЉжЦдьетжжМЭФюЛЈЕЦУПШеЕФзюЕЭжЦдьГЩБОашвЊ648дЊЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉЙлВьБэжаЪ§ОнЃЌЗЂЯжyгыxжЎМфДцдквЛДЮКЏЪ§ЙиЯЕЃЌЩшyЃНkx+bЃЎСаЗНГЬзщЕУЕНyЙигкxЕФКЏЪ§БэДяЪНyЃНЉ2x+100ЃЌИљОнЬтвтЕУЕНwЃНЉ2x2+136xЉ1800ЃЛ
ЃЈ2ЃЉАбwЃНЉ2x2+136xЉ1800ХфЗНЕУЕНwЃНЉ2ЃЈxЉ34ЃЉ2+512ЃЎИљОнЖўДЮКЏЪ§ЕФаджЪМДПЩЕУЕННсТлЃЛ
ЃЈ3ЃЉИљОнЬтвтСаЗНГЬМДПЩЕУЕНМДПЩЃЎ
НтЃКЃЈ1ЃЉЙлВьБэжаЪ§ОнЃЌЗЂЯжyгыxжЎМфДцдквЛДЮКЏЪ§ЙиЯЕЃЌЩшyЃНkx+bЃЎ
дђ![]() ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЌ
ЃЌ
ЁрyЃНЉ2x+100ЃЌ
ЁрyЙигкxЕФКЏЪ§БэДяЪНyЃНЉ2x+100ЃЌ
ЁрwЃНЃЈxЉ18ЃЉyЃНЃЈxЉ18ЃЉЃЈЉ2x+100ЃЉЁрwЃНЉ2x2+136xЉ1800ЃЛ
ЃЈ2ЃЉЁпwЃНЉ2x2+136xЉ1800ЃНЉ2ЃЈxЉ34ЃЉ2+512ЃЎ
ЁрЕБЯњЪлЕЅМлЮЊ34дЊЪБЃЌ
ЁрУПШеФмЛёЕУзюДѓРћШѓ512дЊЃЛ
ЃЈ3ЃЉЕБwЃН350ЪБЃЌ350ЃНЉ2x2+136xЉ1800ЃЌ
НтЕУxЃН25Лђ43ЃЌ
гЩЬтвтПЩЕУ25ЁмxЁм32ЃЌ
дђЕБxЃН32ЪБЃЌ18ЃЈЉ2x+100ЃЉЃН648ЃЌ
ЁржЦдьетжжМЭФюЛЈЕЦУПШеЕФзюЕЭжЦдьГЩБОашвЊ648дЊЃЎ

ЁОЬтФПЁПбЇаЃМЦЛЎЙКТђФГжжЪїУчТЬЛЏаЃдАЃЌМзЁЂввСНСжГЁетжжЪїУчЕФЪлМлЖМЪЧУППУ20дЊЃЌгжИїгаВЛЭЌЕФгХЛнЗНАИЃЌМзСжГЁЃКШєвЛДЮЙКТђ20ПУвдЩЯЃЌЪлМлЪЧУППУ18дЊЃЛввСжГЁЃКШєвЛДЮЙКТђ10ПУвдЩЯЃЌГЌЙ§10ПУВПЗжДђ8.5елЁЃЩшбЇаЃвЛДЮЙКТђетжжЪїУчxПУЃЈxЪЧе§ећЪ§ЃЉ.
ЃЈЂёЃЉИљОнЬтвтЬюаДЯТБэЃК
бЇаЃвЛДЮЙКТђЪїУчЃЈПУЃЉ | 10 | 15 | 20 | 40 |
дкМзСжГЁЪЕМЪЛЈЗбЃЈдЊЃЉ | 200 | 300 | ||
дкввСжГЁЪЕМЪЛЈЗбЃЈдЊЃЉ | 200 | 370 | 710 |
ЃЈЂђЃЉбЇаЃдкМзСжГЁвЛДЮЙКТђЪїУчЃЌЪЕМЪЛЈЗбМЧЮЊ![]() ЃЈдЊЃЉЃЌдкввСжГЁвЛДЮЙКТђЪїУчЃЌЪЕМЪЛЈЗбМЧЮЊ
ЃЈдЊЃЉЃЌдкввСжГЁвЛДЮЙКТђЪїУчЃЌЪЕМЪЛЈЗбМЧЮЊ![]() ЃЈдЊЃЉЃЌЧыЗжБ№аДГі
ЃЈдЊЃЉЃЌЧыЗжБ№аДГі![]() гыxЕФКЏЪ§ЙиЯЕЪНЃЛ
гыxЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈЂѓЃЉЕБ![]() ЪБЃЌбЇаЃдкФФИіСжГЁвЛДЮЙКТђЪїУчЃЌЪЕМЪЛЈЗбНЯЩйЃПЮЊЪВУДЃП
ЪБЃЌбЇаЃдкФФИіСжГЁвЛДЮЙКТђЪїУчЃЌЪЕМЪЛЈЗбНЯЩйЃПЮЊЪВУДЃП