题目内容
6.如图,射线OC以∠AOB的边OB为始边进行逆时针旋转,作OD平分∠AOC,OE平分∠BOC,在射线OC旋转过程中,试探究∠DOE与∠BOC的大小关系.(1)当∠AOB=90°,∠BOC=60°时,则∠DOE=45度.
(2)设∠AOB=90°,∠BOC=n.
①当0<n<90°时,在射线OC旋转过程中,∠DOE的大小是否发生变化?若发生变化,请说明理由;若不发生变化,请求出∠DOE的度数;
②当90°<n<360°时,在射线OC旋转过程中,∠DOE的大小是否发生变化?若发生变化,请说明理由;若不发生变化,请求出∠DOE的度数;
(3)设∠AOB=a,∠BOC=n,其中0<a<180°,在射线OC旋转过程中,请直接写出∠DOE的度数(可用含有a,n的代数式表示)
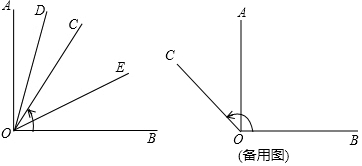
分析 (1)根据角平分线的定义,OD、OE分别平分∠AOC和∠BOC,则可求得∠COE、∠COD的值,∠DOE=∠COE+∠COD;
(2)①结合角的特点,∠DOE=∠DOC+∠COE,求得结果进行判断和计算;②分三种情况讨论:当90°<n≤180°时,当180°<n≤270°时,当270°<n<360°,分别求得∠DOE的度数;
(3)根据(2)中方法进行分类讨论,即可得出∠DOE的度数.
解答 解:(1)∵OD、OE分别平分∠AOC和∠BOC,
∴∠COE=$\frac{1}{2}$∠COB=30°,∠COD=$\frac{1}{2}$∠AOC=15°,
∴∠DOE=∠COE+∠COD=45°;
故答案为:45°;
(2)①∠DOE的大小不变,等于45°,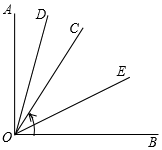
理由:∵OD平分∠AOC,OE平分∠BOC,
∴∠DOE=∠DOC+∠COE
=$\frac{1}{2}$∠BOC+$\frac{1}{2}$∠AOC
=$\frac{1}{2}$(∠AOC+∠BOC)
=$\frac{1}{2}$∠AOB
=$\frac{1}{2}$×90°
=45°;
②分三种情况: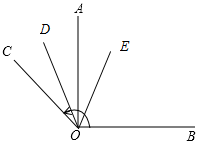
当90°<n≤180°时,∠DOE的大小不变,等于45°,
理由:如图所示,∵OD平分∠AOC,OE平分∠BOC,
∴∠DOE=∠COE-∠DOC
=$\frac{1}{2}$∠BOC-$\frac{1}{2}$∠AOC
=$\frac{1}{2}$(∠BOC-∠AOC)
=$\frac{1}{2}$∠AOB
=$\frac{1}{2}$×90°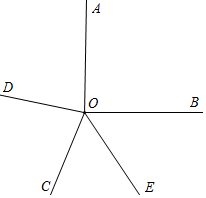
=45°;
当180°<n≤270°时,∠DOE的大小不变,等于135°,
理由:如图所示,∵OD平分∠AOC,OE平分∠BOC,
∴∠DOE=∠COE+∠DOC
=$\frac{1}{2}$∠BOC+$\frac{1}{2}$∠AOC
=$\frac{1}{2}$(∠BOC+∠AOC)
=$\frac{1}{2}$(360°-∠AOB)
=$\frac{1}{2}$×270°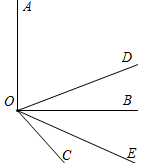
=135°;
当270°<n<360°时,∠DOE的大小不变,等于45°,
理由:如图所示,∵OD平分∠AOC,OE平分∠BOC,
∴∠DOE=∠DOC-∠COE
=$\frac{1}{2}$∠AOC-$\frac{1}{2}$∠BOC
=$\frac{1}{2}$(∠AOC-∠BOC)
=$\frac{1}{2}$∠AOB
=$\frac{1}{2}$×90°
=45°;
(3)在射线OC旋转过程中,∠DOE的度数为$\frac{1}{2}$a或180°-$\frac{1}{2}$a.
理由:当0<n≤180°时,∠DOE=$\frac{1}{2}$a;
当180°<n≤180°+a时,∠DOE=180°-$\frac{1}{2}$a;
当180°+a<n<360°时,∠DOE=$\frac{1}{2}$a;
综上所述,∠DOE的度数为$\frac{1}{2}$a或180°-$\frac{1}{2}$a.
点评 本题主要考查了角的和差关系的运用以及角平分线的定义的运用,即从一个角的顶点出发,把这个角分成相等的两个角的射线叫做这个角的平分线.解决问题的关键是画出图形进行分类讨论,分类时注意不能遗漏,也不能重复.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 0.358×105 | B. | 3.58×104 | C. | 35.8×103 | D. | 358×102 |
 如图,已知△ABC≌△DEF,点B与点E是对应点,点A与点D是对应点,下列说法不一定成立的是( )
如图,已知△ABC≌△DEF,点B与点E是对应点,点A与点D是对应点,下列说法不一定成立的是( )| A. | AB=DE | B. | AC=DF | C. | BE=EC | D. | BE=CF |
| A. | $\left\{\begin{array}{l}{x=0}\\{y=1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=1}\\{y=-1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=1}\\{y=0}\end{array}\right.$ |
| A. | 3x+2x2=5x2 | B. | -ab-ab=-2ab | C. | 2a2b-a2b=1 | D. | 7x+5x=12x2 |
 如图,AB∥GH∥CD,点H在BC上,AC与BD交于点G,AB=2,CD=3,则GH长为( )
如图,AB∥GH∥CD,点H在BC上,AC与BD交于点G,AB=2,CD=3,则GH长为( )| A. | 1 | B. | 1.2 | C. | 2 | D. | 2.5 |
| A. | x≠8 | B. | x<8 | C. | x≤8 | D. | x>0且x≠8 |