题目内容
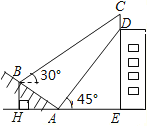
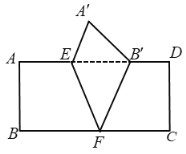
【题目】如图，把矩形
沿
翻折，点
恰好落在
边的
处，若
，
，
，则矩形的面积是（ ）
A.
B.
C.
D.16
【答案】A
【解析】
由折叠的性质和矩形的性质可得：
=∠
=60°，进而可得△
是等边三角形，可得
，连接BE，如图，则△BEF是等边三角形，可得∠EBF=60°，从而得∠ABE=30°，于是在Rt△ABE中解直角三角形可求出AB的长，然后根据矩形的面积公式即可求出结果．
解：∵把矩形
沿
翻折，点
恰好落在
边的
处，
∴∠BFE==60°，
∵四边形ABCD是矩形，
∴AD∥BC，
∴∠=∠BFE=60°，
∴△是等边三角形，
∴，
连接BE，如图，则△BEF是等边三角形，
∴∠EBF=60°，
∴∠ABE=30°，
∴
，
∵AD=AE+DE=3+8=11，
∴矩形的面积=AB×AD=
．
故选：A．
【题目】2019年5月，“亚洲文明对话大会”在北京成功举办，某研究机构为了了解10-60岁年年龄段市民对本次大会的关注程度，随机选取了100名年龄在该范围内的市民进行了调查，并将搜集到的数据制成了尚不完整的频数分布表、频数分布直方图和扇形统计图，如下所示：
组别 | 年龄段 | 频数（人数） |
第一组 |
| 5 |
第二组 |
|
|
第三组 |
| 35 |
第四组 |
| 20 |
第五组 |
| 15 |
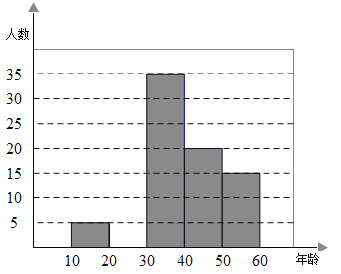
请直接写出第3组人数在扇形统计图中所对应的圆心角是_________度；假设该市现有10-60岁的市民300万人，则40-50岁年龄段的关注本次大会的人数约有___________万人．
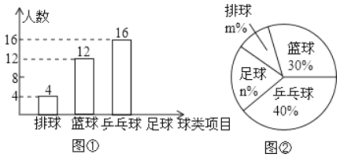
【题目】2015年某省为加快建设综合交通体系，对铁路、公路、机场三个重大项目加大建设资金的投入．
（1）机场建设项目中所有6个机场投入的建设资金金额统计如下图，已知机场
投入的建设资金金额是机场
、
所投入建设资金金额之和的三分之二，求机场投入的建设资金金额是多少亿元？并补全条形统计图．
（2）将铁路、公路、机场三项建设所投入的资金金额绘制成如下扇形统计图以及统计表，根据扇形统计图及统计表中的信息，求得
；
；
；
；
．（请直接填写计算结果）
铁路 | 公路 | 机场 | 铁路、公路、机场三项投入建设资金总金额（亿元） | |
投入资金（亿元） | 300 |
|
|
|
所占百分比 |
| 34% | 6% | |
所占圆心角 |
|
|
|
【题目】为缓解油价上涨给出租车行业带来的成本压力，某市调整出租车运价，调整方案见下列表格及图象（其中
、
、
为常数）：
行驶路程 | 收费标准 | |
调价前 | 调价后 | |
不超出 | 起步价9元 | 起步价 |
超出 | 每公里2元 | 每公里 |
超出 | 每公里 | |
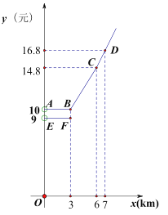
设行驶路程为
时，调价前的运价为
（元），调价后的运价为
（元）．如图，折线
表示与
之间的函数关系；线段
表示
时，与之间的函数关系．根据图表信息，完成下列各题：
（1）填空：
_____，
_____，
_______；
（2）写出当
时，与之间的函数关系式，并在上图中画出该函数图象；
（3）当行驶路程为时，讨论调价前后运价的高低．
【题目】如图，P是弧AB所对弦AB上一动点，过点P作PM⊥AB交AB于点M，连接MB，过点P作PN⊥MB于点N.已知AB =6cm，设A 、P两点间的距离为xcm，P、N两点间的距离为ycm.（当点P与点A或点B重合时，y的值为0）
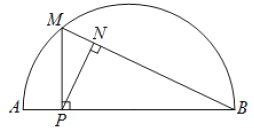
小东根据学习函数的经验，对函数y随自变量x的变化而变化的规律进行了探究．
下面是小东的探究过程，请补充完整：
（1）通过取点、画图、测量，得到了x与y的几组值，如下表：
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y/cm | 0 | 2.0 | 2.3 | 2.1 | 0.9 | 0 |
（说明：补全表格时相关数值保留一位小数）
（2）建立平面直角坐标系，描出以补全后的表中各对对应值为坐标的点，画出该函数的图象.
（3）结合画出的函数图象，解决问题：当△PAN为等腰三角形时，AP的长度约为____________cm.
