题目内容
2.设一元二次方程(2x-3)(x+2)-12=0的两个实数根为x1,x2,求(x${\;}_{1}+\frac{1}{{x}_{2}}$)(x${\;}_{2}+\frac{1}{{x}_{1}}$)的值.分析 首先把方程化为一般形式为2x2+x-18=0,利用根与系数的关系得出x1•x2=-9,再进一步整理代入求得答案即可.
解答 解:原方程化为一般形式为2x2+x-18=0,
则x1+x2=-$\frac{1}{2}$,x1•x2=-9,
(x${\;}_{1}+\frac{1}{{x}_{2}}$)(x${\;}_{2}+\frac{1}{{x}_{1}}$)
=x1•x2+$\frac{1}{{x}_{1}{x}_{2}}$+2
=-9-$\frac{1}{9}$+2
=-7$\frac{1}{9}$.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0)的根与系数的关系,若方程ax2+bx+c=0两个根为x1,x2,则x1+x2=-$\frac{b}{a}$,x1•x2=$\frac{c}{a}$,渗透整体代入的思想.

练习册系列答案
相关题目
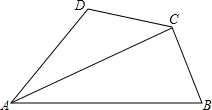 已知,四边形ABCD中,∠D与∠B互补,且对角线AC平分∠BAD,请比较BC与DC的大小,并证明你的结论.
已知,四边形ABCD中,∠D与∠B互补,且对角线AC平分∠BAD,请比较BC与DC的大小,并证明你的结论. 已知:如图,在△ABC中,∠BCA=2∠B,D为∠BCA的平分线上的-点,连结AD,∠D=∠B.求证:AD∥BC.
已知:如图,在△ABC中,∠BCA=2∠B,D为∠BCA的平分线上的-点,连结AD,∠D=∠B.求证:AD∥BC.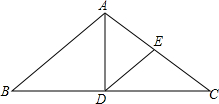 如图所示,已知:△ABC中,AB=AC,D是BC的中点,E是AC的中点,若∠EDC=∠C,BC=32cm,DE=10cm,求△ABC的面积.
如图所示,已知:△ABC中,AB=AC,D是BC的中点,E是AC的中点,若∠EDC=∠C,BC=32cm,DE=10cm,求△ABC的面积. 如图所示,a1、a2、a3的大小关系是a1>a2>a3.
如图所示,a1、a2、a3的大小关系是a1>a2>a3.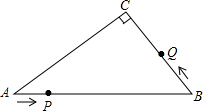 如图,在Rt△ABC中,∠C=90°,AB=10cm,AC:BC=4:3,点P从点A出发沿AB方向向点B运动,速度为1cm/s,同时点Q从点B出发沿B→C→A方向向点A运动,速度为2cm/s,当一个运动点到达终点时,另一个运动点也随之停止运动.
如图,在Rt△ABC中,∠C=90°,AB=10cm,AC:BC=4:3,点P从点A出发沿AB方向向点B运动,速度为1cm/s,同时点Q从点B出发沿B→C→A方向向点A运动,速度为2cm/s,当一个运动点到达终点时,另一个运动点也随之停止运动.