题目内容
11.先化简,再求值:$\frac{{a}^{2}-{b}^{2}}{{a}^{2}b-a{b}^{2}}$÷(1+$\frac{{a}^{2}+{b}^{2}}{2ab}$),其中a=8-$\sqrt{13}$,b=-5+2$\sqrt{13}$.
分析 先根据分式混合运算的法则把原式进行化简,再把a,b的值代入进行计算即可.
解答 解:原式=$\frac{(a+b)(a-b)}{ab(a-b)}$÷$\frac{(a+b)^{2}}{2ab}$
=$\frac{a+b}{ab}$•$\frac{2ab}{(a+b)^{2}}$
=$\frac{2}{a+b}$,
当a=8-$\sqrt{13}$,b=-5+2$\sqrt{13}$时,原式=$\frac{2}{8-\sqrt{13}-5+2\sqrt{13}}$=$\frac{2}{3+\sqrt{13}}$=$\frac{\sqrt{13}-3}{2}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
相关题目
 如图,
如图,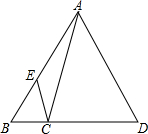 如图.已知CD=2BC,AE=2BE,则三角形BEC的面积和三角形ABD的面积比是$\frac{1}{9}$.
如图.已知CD=2BC,AE=2BE,则三角形BEC的面积和三角形ABD的面积比是$\frac{1}{9}$.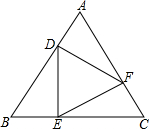 如图,在等边△ABC中,D、E、F三点分别在AB,BC,AC上,DE⊥BC于E,EF⊥AC于F,FD⊥AB于D.
如图,在等边△ABC中,D、E、F三点分别在AB,BC,AC上,DE⊥BC于E,EF⊥AC于F,FD⊥AB于D.