题目内容
14. 若函数y=kx+b的图象如图所示,那么当y>0时,x的取值范围是( )
若函数y=kx+b的图象如图所示,那么当y>0时,x的取值范围是( )| A. | x>1 | B. | x>2 | C. | x<1 | D. | x<2 |
分析 根据函数图象与x轴的交点坐标,当y>0即图象在x轴上方,求出即可.
解答 解:因为直线y=kx+b与x轴的交点坐标为(2,0),
由函数的图象可知x<2时,图象在x轴上方,即y>0,
所以当y>0时,x<2.
故选D.
点评 本题考查了一次函数与一元一次不等式:从函数的角度看,就是寻求使一次函数y=ax+b的值大于(或小于)0的自变量x的取值范围;从函数图象的角度看,就是确定直线y=kx+b在x轴上(或下)方部分所有的点的横坐标所构成的集合.

练习册系列答案
相关题目
6.四边形ABCD中,对角线AC、BD相交于点O,给出下列四个条件:①AD∥BC;②AD=BC;③OA=OC;④OB=OD,从中任选两个条件,能使四边形ABCD为平行四边形的选法有( )
| A. | 6种 | B. | 5种 | C. | 4种 | D. | 3种 |
3.为筹备班级联欢会,班干部对全班同学最爱吃的水果进行了统计,最终决定买哪种水果时,班干部最关心的统计量是( )
| A. | 平均数 | B. | 中位数 | C. | 众数 | D. | 方差 |
4.a,b是两个连续整数,若a<$\sqrt{8}$<b,则a,b分别是( )
| A. | 3,2 | B. | 3,4 | C. | 2,3 | D. | 7,9 |
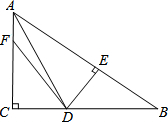 如图,已知△ABC中,∠C=90°,AD平分∠BAC交BC于D,DE⊥AB于E,点F在AC上,且BD=FD,求证:AE-BE=AF.
如图,已知△ABC中,∠C=90°,AD平分∠BAC交BC于D,DE⊥AB于E,点F在AC上,且BD=FD,求证:AE-BE=AF. 一个正方形和两个等边三角形的位置如图所示,∠3=55°,则∠1+∠2=95°.
一个正方形和两个等边三角形的位置如图所示,∠3=55°,则∠1+∠2=95°. 如图,在每个小正方形边长为1的方格纸中,△ABC的顶点都在方格纸格点上.将△ABC向左平移2格,再向上平移4格.
如图,在每个小正方形边长为1的方格纸中,△ABC的顶点都在方格纸格点上.将△ABC向左平移2格,再向上平移4格.