题目内容
4.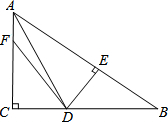 如图,已知△ABC中,∠C=90°,AD平分∠BAC交BC于D,DE⊥AB于E,点F在AC上,且BD=FD,求证:AE-BE=AF.
如图,已知△ABC中,∠C=90°,AD平分∠BAC交BC于D,DE⊥AB于E,点F在AC上,且BD=FD,求证:AE-BE=AF.
分析 根据角平分线的性质得出DC=DE,再根据全等三角形的判定得出△ACD≌△AED,△FCD≌△BED,进而得出AC=AE,CF=BE,最后利用线段的和差解答即可.
解答 证明:∵AD平分∠BAC交BC于D,DE⊥AB于E,∠C=90°,
∴DC=DE,
在Rt△ACD和Rt△AED中,
$\left\{\begin{array}{l}{DC=DE}\\{AC=AC}\end{array}\right.$,
∴Rt△ACD≌Rt△AED(HL),
同理可得Rt△FCD和Rt△BED,
∴AC=AE,CF=BE,
∴AE-BE=AF.
点评 本题考查了角平分线的性质,关键是根据全等三角形的判定和性质证明.

练习册系列答案
相关题目
12.下列方程为一元一次方程的是( )
| A. | y=0 | B. | 3x+2y=3 | C. | x2=2x | D. | $\frac{1}{y}+y=2$ |
19.某种感冒病毒的直径为0.0000000031米,用科学记数法表示为( )
| A. | 3.1×10-10米 | B. | 3.1×10-9米 | C. | -3.1×109米 | D. | 0.31×10-8米 |
9.根据下表中的对应值,判断一元二次方程x2-4x+2=0的一个解的取值范围是0.5<x<1.
| x | 0 | 0.5 | 1 | 1.5 |
| x2-4x+2 | 2 | 0.25 | -1 | -1.75 |
16.为了解本区初中学生的视力情况,教育局有关部门采用抽样调查的方法,从全区2万名中学生中抽查了部分学生的视力,分成如表四类进行统计
注:(4.3-4.5之间表示包括4.3及4.5)
根据图表完成下列问题:
(1)填完整表格及补充完整图一;
(2)“类型D”在扇形图(图二)中所占的圆心角是162度;
(3)本次调查数据的中位数落在C类型内;
(4)视力在5.0以下(不含5.0)均为不良,那么全区视力不良的初中学生估计11000人.
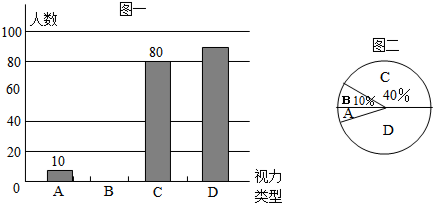
| 视力 | 类型 | 人数 |
| 视力在4.2及以下 | A | 10 |
| 视力在4.3-4.5之间 | B | 20 |
| 视力在4.6-4.9之间 | C | |
| 视力在5.0及以上 | D |
根据图表完成下列问题:
(1)填完整表格及补充完整图一;
(2)“类型D”在扇形图(图二)中所占的圆心角是162度;
(3)本次调查数据的中位数落在C类型内;
(4)视力在5.0以下(不含5.0)均为不良,那么全区视力不良的初中学生估计11000人.

14. 若函数y=kx+b的图象如图所示,那么当y>0时,x的取值范围是( )
若函数y=kx+b的图象如图所示,那么当y>0时,x的取值范围是( )
 若函数y=kx+b的图象如图所示,那么当y>0时,x的取值范围是( )
若函数y=kx+b的图象如图所示,那么当y>0时,x的取值范围是( )| A. | x>1 | B. | x>2 | C. | x<1 | D. | x<2 |