题目内容
7. 如图,在平面直角坐标系xOy中,矩形OABC的两边OC、OA分别在x轴、y轴的正半轴上,反比例函数y=$\frac{k}{x}$(x>0)与AB相交于点D,与BC相交于点E,若BE=4EC,且△ODE的面积是5,则k的值为$\frac{25}{12}$.
如图,在平面直角坐标系xOy中,矩形OABC的两边OC、OA分别在x轴、y轴的正半轴上,反比例函数y=$\frac{k}{x}$(x>0)与AB相交于点D,与BC相交于点E,若BE=4EC,且△ODE的面积是5,则k的值为$\frac{25}{12}$.
分析 设B点的坐标为(a,b),根据矩形的性质以及BE=4EC,表示出E、D两点的坐标,根据S△ODE=S矩形OCBA-S△AOD-S△OCE-S△BDE=5,求出B的横纵坐标的积,进而求出反比例函数的比例系数.
解答  解:∵四边形OCBA是矩形,
解:∵四边形OCBA是矩形,
∴AB=OC,OA=BC,
设B点的坐标为(a,b),
∵BE=4EC,
∴E(a,$\frac{1}{5}$b),
∵点D,E在反比例函数的图象上,
∴a•$\frac{1}{5}$b=k,∴D($\frac{1}{5}$a,b),
∵S△ODE=S矩形OCBA-S△AOD-S△OCE-S△BDE
=ab-$\frac{1}{2}$•$\frac{1}{5}$a•b-$\frac{1}{2}$•a•$\frac{1}{5}$b-$\frac{1}{2}$•(a-$\frac{1}{5}$a)•(b-$\frac{1}{5}$b)
=$\frac{12}{25}$ab=5,
∴ab=$\frac{125}{12}$,
∴k=$\frac{1}{5}$ab=$\frac{25}{12}$.
故答案为$\frac{25}{12}$.
点评 此题考查了矩形的性质,反比例函数图象上点的坐标特征,反比例函数比例系数k的几何意义,设B点的坐标为(a,b),根据S△ODE=S矩形OCBA-S△AOD-S△OCE-S△BDE=5,求出ab的值是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.下列各式
(1)b5•b5=2b5
(2)(-2a2)2=-4a4
(3)(an-1)3=a3n-1
(4)2m+3n=6m+n
(5)(a-b)5(b-a)4=(a-b)20
(6)-a3•(-a)5=a8
其中计算错误的有( )
(1)b5•b5=2b5
(2)(-2a2)2=-4a4
(3)(an-1)3=a3n-1
(4)2m+3n=6m+n
(5)(a-b)5(b-a)4=(a-b)20
(6)-a3•(-a)5=a8
其中计算错误的有( )
| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
16.某数学老师为了了解学生在数学学习中常见错误的纠正情况,收集了学生在作业和考试中的常见错误,编制了10道选择题,每题3分,对自己所任教的八年级(1)班和(2)班进行了检测.如下两组数据表示从两班各随机抽取的10名学生的得分情况:(单位:分)
(1)班:24,21,27,24,21,27,21,24,27,24.
(2)班:24,21,30,21,27,15,27,21,24,30.
(1)利用图中提供的信息,补全下表:
(2)若把24分以上记为“优秀”,两班各有60名学生,请估计两班各有多少名学生成绩优秀.
(1)班:24,21,27,24,21,27,21,24,27,24.
(2)班:24,21,30,21,27,15,27,21,24,30.
(1)利用图中提供的信息,补全下表:
| 班级 | 平均数(分) | 中位数(分) | 众数(分) |
| (1)班 | 24 | 24 | 24 |
| (2)班 | 24 | 24 | 21 |
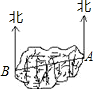 如图,A、B之间是一座山,一条高速公路要通过A、B两点,在A地测得公路走向是北偏西111°32′.如果A、B两地同时开工,那么在B地按北偏东68°28′方向施工,才能使公路在山腹中准确接通.
如图,A、B之间是一座山,一条高速公路要通过A、B两点,在A地测得公路走向是北偏西111°32′.如果A、B两地同时开工,那么在B地按北偏东68°28′方向施工,才能使公路在山腹中准确接通.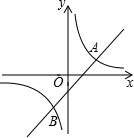 在平面直角坐标系中,直线y1=x+m与双曲线y2=$\frac{k}{x}$交于点A、B,已知点A、B的横坐标为2和-1.
在平面直角坐标系中,直线y1=x+m与双曲线y2=$\frac{k}{x}$交于点A、B,已知点A、B的横坐标为2和-1.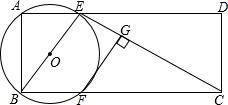 如图,在矩形ABCD中,AB=2,AD=5,过点A、B作⊙O,交AD、BC于点E、F,连接BE、CE,过点F作FG⊥CE,垂足为G.
如图,在矩形ABCD中,AB=2,AD=5,过点A、B作⊙O,交AD、BC于点E、F,连接BE、CE,过点F作FG⊥CE,垂足为G.