题目内容
17.已知$\frac{b}{a}$=$\frac{5}{13}$,则$\frac{a-b}{a+b}$的值是( )| A. | $\frac{8}{13}$ | B. | $\frac{5}{8}$ | C. | $\frac{4}{9}$ | D. | $\frac{9}{4}$ |
分析 根据等式的性质,可用a表示b,根据分式的性质,可得答案.
解答 解:由$\frac{b}{a}$=$\frac{5}{13}$,得
b=$\frac{5}{13}$a.
$\frac{a-b}{a+b}$=$\frac{a-\frac{5}{13}a}{a+\frac{5}{13}a}$=$\frac{4}{9}$,
故选:C.
点评 本题考查了比例的性质,利用等式的性质得出b=$\frac{5}{13}$a是解题关键.

练习册系列答案
相关题目
5.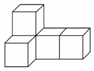 如图,它是由5个完全相同的小正方体搭建的几何体,若将最右边的小正方体拿走,则下列结论正确的是( )
如图,它是由5个完全相同的小正方体搭建的几何体,若将最右边的小正方体拿走,则下列结论正确的是( )
 如图,它是由5个完全相同的小正方体搭建的几何体,若将最右边的小正方体拿走,则下列结论正确的是( )
如图,它是由5个完全相同的小正方体搭建的几何体,若将最右边的小正方体拿走,则下列结论正确的是( )| A. | 主视图不变 | B. | 左视图不变 | C. | 俯视图不变 | D. | 三视图都不变 |
12.判断下列几组数据中,可以作为直角三角形的三条边的是( )
| A. | 1,2,3 | B. | 2,3,4 | C. | 3,4,5 | D. | 4,5,6 |
2.一个不透明的盒子有有n个除颜色外其它完全相同的小球,其中有6个黄球,每次摸球前先将盒子里的球摇匀,任意摸出一个球记下颜色后在放回盒子,通过大量重复摸球实验后发现,摸到黄球的频率稳定在20%,那么可以推算出n大约是( )
| A. | 30 | B. | 20 | C. | 12 | D. | 6 |
6.李刚同学的四次数学测试成绩分别是80分、76分、90分、84分,如果按照1:2:4:1的权重对这四次成绩进行综合评价,李刚同学的综合得分应是( )
| A. | 84.5分 | B. | 85分 | C. | 84分 | D. | 83分 |
7.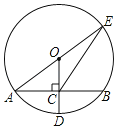 如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,CD=2,则EC的长为( )
如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,CD=2,则EC的长为( )
 如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,CD=2,则EC的长为( )
如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,CD=2,则EC的长为( )| A. | 2$\sqrt{10}$ | B. | 2$\sqrt{13}$ | C. | 2$\sqrt{15}$ | D. | 8 |
