Question

2．平面上有3个点的坐标：A（0，-3），B（3，0），C（-1，-4）． 
（1）在A，B，C三个点中任取一个点，这个点既在直线y₁=x-3上又在抛物线上y₂=x²-2x-3上的概率是多少？
（2）从A，B，C三个点中任取两个点，求两点都落在抛物线y₂=x²-2x-3上的概率．

Answer 1

分析 （1）先根据一次函数图象上点的坐标特征和二次函数图象上点的坐标特征可判断A、B、C都在直线上，A、B两点在抛物线上，C点不在抛物线上，然后根据概率公式求解；
（2）先画树状图展示所有6种等可能的结果数，再找出两点都落在抛物线y₂=x²-2x-3上的结果数，然后根据概率公式求解．

解答 解：（1）当x=0时，y₁=x-3=-3，y₂=x²-2x-3=-3，则A点在直线和抛物线上；
当x=3时，y₁=x-3=0，y₂=x²-2x-3=0，则B点在直线和抛物线上；
当x=-1时，y₁=x-3=-4，y₂=x²-2x-3=0，则C点在直线上，不在抛物线上，
所以在A，B，C三个点中任取一个点，这个点既在直线y₁=x-3上又在抛物线上y₂=x²-2x-3上的概率=$\frac{2}{3}$；
（2）画树状图为：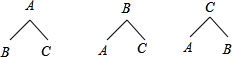

共有6种等可能的结果数，其中两点都落在抛物线y₂=x²-2x-3上的结果数为2，
所以两点都落在抛物线y₂=x²-2x-3上的概率=$\frac{2}{6}$=$\frac{1}{3}$．

点评 本题考查了列表法或树状图法：通过列表法或树状图法展示所有等可能的结果求出n，再从中选出符合事件A或B的结果数目m，然后根据概率公式求出事件A或B的概率．也考查了一次函数图象上点的坐标特征和二次函数图象上点的坐标特征．