题目内容
12.如图,当四边形ABCD的内部有一个点P1时,最多可以把四边形ABCD剪成4个三角形,当四边形ABCD内部有两个点P1,P2时,最多可以把四边形剪6个三角形;(1)当四边形ABCD的内部有3个点P1、P2、P3时,最多可把它剪成8个三角形;
(2)当四边形ABCD的内部有10个点P1…P10时,最多可把它剪成22个三角形;
当四边形ABCD内部有n个点P1…Pn时,最多可以把它剪成2(n+1)个三角形;
(3)最多可以把四边形ABCD剪成2016个三角形吗?若能,求出四边形ABCD内部有多少个点?若不能,请说明理由;
(4)若设四边形ABCD的内部分别有1个点时,最多可以把四边形ABCD剪成S1个三角形;有2个点时,最多可以把四边形ABCD剪成S2个三角形;…有100个点时,最多可以把四边形ABCD剪成S100个三角形;求S1+S2+…+S100的值.

分析 根据四边形中1个点时,最多分割成的三角形的个数是4,四边形中2个点时,最多分割成的三角形的个数是4+2×1,四边形中3个点时,最多分割成的三角形的个数是4+2×2,得出规律即可,
(1)根据规律即可得出结论;
(2)根据规律即可得出结论;
(3)假设可以,建立方程求解,最后判断即可;
(4)先列出式子,再求和即可.
解答 解:∵四边形中1个点时,最多分割成的三角形的个数是4,
四边形中2个点时,最多分割成的三角形的个数是4+2×1,
四边形中3个点时,最多分割成的三角形的个数是4+2×2,
四边形中4个点时,最多分割成的三角形的个数是4+2×3,
…,
∴四边形中n个点时,最多分割成的三角形的个数是4+2(n-1)=2n+2=2(n+1),
(1)当四边形ABCD的内部有3个点时,n=3,
∴2(n+1)=2(3+1)=8,
故答案为8;
(2)当四边形ABCD的内部有10个点时,n=10,
∴2(n+1)=2(10+1)=22,
故答案为22;
(3)最多可以把四边形ABCD剪成2016个三角形,
假设最多可以把四边形ABCD剪成2016个三角形,
∴2(n+1)=2016,
∴n=1007,
∴四边形ABCD内部有1007个点;
(4)根据题意得,S1=4,S2=4+2×1,S3=4+2×2,S4=4+2×3,S5=4+2×4,S100=4+2×99,
∴S1+S2+…+S100=4+(4+2×1)+(4+2×2)+(4+4×3)+…+(4+2×99)
=4×100+(2×1+2×2+2×3+2×4+…+2×99)
=400+2(1+2+3+4+…+99)
=400+2×$\frac{99×(1+99)}{2}$
=400+9900
=10300.
点评 此题是图形的变化类问题,根据数据的变化规律,结合图形,总结出每增加一个点,三角形的个数最多增加2的规律是解题的关键.

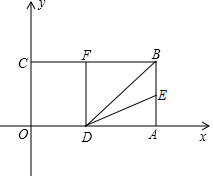 如图,以长方形OABC的顶点O为原点,OA所在直线为x轴,OC所在直线为y轴,建立平面直角坐标系.已知OA=3,OC=2,点E是AB的中点,在OA上取一点D,连结BD,点A关于BD的对称点恰好落在线段BC边上的点F处.
如图,以长方形OABC的顶点O为原点,OA所在直线为x轴,OC所在直线为y轴,建立平面直角坐标系.已知OA=3,OC=2,点E是AB的中点,在OA上取一点D,连结BD,点A关于BD的对称点恰好落在线段BC边上的点F处.
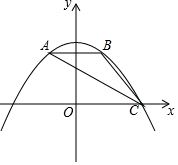 如图,抛物线y=ax2+$\frac{9}{4}$经过△ABC的三个顶点,点A坐标为(-1,2),点B是点A关于y轴的对称点,点C在x轴的正半轴上.
如图,抛物线y=ax2+$\frac{9}{4}$经过△ABC的三个顶点,点A坐标为(-1,2),点B是点A关于y轴的对称点,点C在x轴的正半轴上.
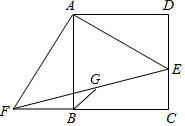 E为正方形ABCD的边CD上一点,将△ADE绕A点顺时针旋转90°,得△ABF,G为EF中点.下列结论:①G在△ABF的外接圆上;②EC=$\sqrt{2}$BG;③B,G,D三点在同一条直线上;④若S四边形BGEC=$\frac{1}{4}$S正方形ABCD,那么E为DC的黄金分割点.正确的是( )
E为正方形ABCD的边CD上一点,将△ADE绕A点顺时针旋转90°,得△ABF,G为EF中点.下列结论:①G在△ABF的外接圆上;②EC=$\sqrt{2}$BG;③B,G,D三点在同一条直线上;④若S四边形BGEC=$\frac{1}{4}$S正方形ABCD,那么E为DC的黄金分割点.正确的是( ) 已知抛物线y=-x2+bx+3交x轴负、正半轴于A、B两点,交y轴与点C,且tan∠ACO=$\frac{1}{3}$,△ABC的外接圆的圆心为M.
已知抛物线y=-x2+bx+3交x轴负、正半轴于A、B两点,交y轴与点C,且tan∠ACO=$\frac{1}{3}$,△ABC的外接圆的圆心为M.