题目内容
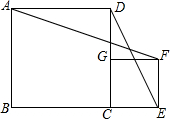 已知正方形ABCD与CEFG的边长分别为a、b,连结DE、AF.固定正方形ABCD,将正方形CEFG绕定点C逆时针旋转角度α度(0<α<180).设DE=x,AF=y.
已知正方形ABCD与CEFG的边长分别为a、b,连结DE、AF.固定正方形ABCD,将正方形CEFG绕定点C逆时针旋转角度α度(0<α<180).设DE=x,AF=y.(1)若a=4cm,b=2cm,求旋转过程中y的取值范围;
(2)对于旋转角度为锐角和钝角两种情况,画出图象;
(3)探究y与x的函数关系式.
考点:旋转的性质,正方形的性质
专题:计算题
分析:(1)连接AC,CF,如图,根据正方形的性质得AC=4
cm,CF=2
cm,∠ACD=45°,∠GCF=45°,由于当α=90°时,C、F、A三点共线,此时AF最小,易得最小值=2
cm,当α=0°或180°时,AF最长,利用勾股定理可计算出AF=2
cm,于是得到旋转过程中y的取值范围为2
cm≤y<2
cm;
(2)分两种情况画图;
(3)分类讨论:当0°<α≤90°时,连接AC,CF,如图3,根据旋转的性质得∠DCE=90°-α,∠ACF=90°-α,则∠DCE=∠ACF,由于CD=a,AC=
a,CE=b,CF=
b,则
=
=
,则根据三角形相似的判定方法得到△ACF∽△DCE,所以
=
=
,即y=
x;对于当90°<α<180°时,同样可得y=
x.
| 2 |
| 2 |
| 2 |
| 10 |
| 2 |
| 10 |
(2)分两种情况画图;
(3)分类讨论:当0°<α≤90°时,连接AC,CF,如图3,根据旋转的性质得∠DCE=90°-α,∠ACF=90°-α,则∠DCE=∠ACF,由于CD=a,AC=
| 2 |
| 2 |
| AC |
| CD |
| CF |
| CE |
| 2 |
| AF |
| DE |
| AC |
| CD |
| 2 |
| 2 |
| 2 |
解答: 解:(1)连接AC,CF,如图,
解:(1)连接AC,CF,如图,
∵正方形ABCD与CEFG的边长分别为a=4cm、b=2cm,
∴AC=4
cm,CF=2
cm,∠ACD=45°,∠GCF=45°,
当α=90°时,C、F、A三点共线,此时AF最小,最小值=4
cm-2
cm=2
cm,
当α=0°或180°时,AF最长,此时AF=
=2
(cm),
∴旋转过程中y的取值范围为2
cm≤y<2
cm;
 (2)当0°<α≤90°时,如图1,
(2)当0°<α≤90°时,如图1,
当90°<α<180°时,如图2;
(3)当0°<α≤90°时,连接AC,CF,如图3,
∵正方形CEFG绕定点C逆时针旋转角度α度
∴∠DCE=90°-α,∠ACF=90°-α,
∴∠DCE=∠ACF,
 ∵CD=a,AC=
∵CD=a,AC=
a,CE=b,CF=
b,
∴
=
=
,
∴△ACF∽△DCE,
∴
=
=
,
即
=
,
∴y=
x;
当90°<α<180°时,同样可得y=
x,
∴y与x的函数关系式为y=
x.
 解:(1)连接AC,CF,如图,
解:(1)连接AC,CF,如图,∵正方形ABCD与CEFG的边长分别为a=4cm、b=2cm,
∴AC=4
| 2 |
| 2 |
当α=90°时,C、F、A三点共线,此时AF最小,最小值=4
| 2 |
| 2 |
| 2 |
当α=0°或180°时,AF最长,此时AF=
| AC2+CF2 |
| 10 |
∴旋转过程中y的取值范围为2
| 2 |
| 10 |
 (2)当0°<α≤90°时,如图1,
(2)当0°<α≤90°时,如图1,当90°<α<180°时,如图2;
(3)当0°<α≤90°时,连接AC,CF,如图3,
∵正方形CEFG绕定点C逆时针旋转角度α度
∴∠DCE=90°-α,∠ACF=90°-α,
∴∠DCE=∠ACF,
 ∵CD=a,AC=
∵CD=a,AC=| 2 |
| 2 |
∴
| AC |
| CD |
| CF |
| CE |
| 2 |
∴△ACF∽△DCE,
∴
| AF |
| DE |
| AC |
| CD |
| 2 |
即
| y |
| x |
| 2 |
∴y=
| 2 |
当90°<α<180°时,同样可得y=
| 2 |

∴y与x的函数关系式为y=
| 2 |
点评:本题考查了旋转的性质:旋转前后两图形全等;对应点到旋转中心的距离相等;对应点与旋转中心的连线段的夹角等于旋转角.也考查了正方形的性质.

练习册系列答案
相关题目
小蒋和小潘两人电脑打字比赛,小蒋每分钟比小潘少打8个字,小蒋打800个字和小潘打880个字所用的时间相等.设小蒋打字速度为x个/分钟,则下列方程正确的是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 已知圆锥的底面半径为r=2cm,高h=2
已知圆锥的底面半径为r=2cm,高h=2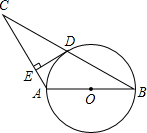 如图,△ABC中,AB=AC,以AB为直径的⊙O交BC于点D.
如图,△ABC中,AB=AC,以AB为直径的⊙O交BC于点D. 我们在分析解决某些数学问题时,经常要比较两个数或代数式的大小.而解决问题的策略一般要进行一定的转化,其中“作差法”就是常用的方法之一.所谓“作差法”:就是通过作差、变形.并利用差的符号来确定它们的大小,即要比较代数式 M、N的大小,只要作出它们的差M-N,若M-N>0,则M>N;若M-N=0,则M=N;若M-N<0;则 M<N.
我们在分析解决某些数学问题时,经常要比较两个数或代数式的大小.而解决问题的策略一般要进行一定的转化,其中“作差法”就是常用的方法之一.所谓“作差法”:就是通过作差、变形.并利用差的符号来确定它们的大小,即要比较代数式 M、N的大小,只要作出它们的差M-N,若M-N>0,则M>N;若M-N=0,则M=N;若M-N<0;则 M<N.