题目内容
已知圆锥的底面半径为r=2cm，高h=2| 15 |
考点：平面展开-最短路径问题,圆锥的计算
专题：
分析：蚂蚁爬行的最短距离是圆锥的侧面展开图的扇形中AA′的长度．根据勾股定理求得母线长后，利用弧长等于底面周长求得扇形的圆心角的度数为90度，再由等腰直角三角形的性质求解．
解答：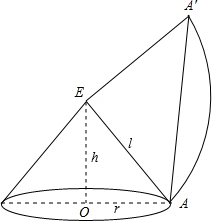
解：如图，设圆锥的顶为E，将圆锥的侧面展开得到一个扇形，设此扇形的圆心角为n°，
∵r=2cm，h=2
cm，
∴由勾股定理可得母线l=
=8cm，
而圆锥侧面展开后的扇形的弧长为2×2π=
，
∴n=90，
即△EAA′是等腰直角三角形，
∴由勾股定理得：AA'=
=8
cm．
答：蚂蚁爬行的最短距离为8
cm．
解：如图，设圆锥的顶为E，将圆锥的侧面展开得到一个扇形，设此扇形的圆心角为n°，∵r=2cm，h=2
| 15 |
∴由勾股定理可得母线l=
| h2+r2 |
而圆锥侧面展开后的扇形的弧长为2×2π=
| nπ×8 |
| 180 |
∴n=90，
即△EAA′是等腰直角三角形，
∴由勾股定理得：AA'=
| A′E2+AE2 |
| 2 |
答：蚂蚁爬行的最短距离为8
| 2 |
点评：本题考查了平面展开-最短路径问题，勾股定理，弧长公式，圆的周长公式，等腰直角三角形的性质，难度适中．
练习册系列答案
华东师大版一课一练系列答案
相关题目
点（-4，y1），（-2，y2），（1，y3）都在反比例函数y=-
的图象上，则（ ）
| 1 |
| x |
| A、y1＞y2＞y3 |
| B、y2＞y1＞y3 |
| C、y3＞yl＞y2 |
| D、y1＞y3＞y2 |
已知线段m、n，且5m=3n，则
等于（ ）
| m |
| n |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知正方形ABCD与CEFG的边长分别为a、b，连结DE、AF．固定正方形ABCD，将正方形CEFG绕定点C逆时针旋转角度α度（0＜α＜180）．设DE=x，AF=y．
如图，在△ABC中，D是BC边的中点，F、E分别是AD及延长线上的点，CF∥BE．