题目内容
10. 如图所示,已知直线$y=\frac{1}{2}x$与双曲线$y=\frac{k}{x}(k>0)$交于A、B两点,其中点B的纵坐标为-2.
如图所示,已知直线$y=\frac{1}{2}x$与双曲线$y=\frac{k}{x}(k>0)$交于A、B两点,其中点B的纵坐标为-2.(1)求双曲线的解析式;
(2)过原点O的另一条直线l在第一象限交$y=\frac{k}{x}(k>0)$于点P (异于点A),直线PA交x轴于点M,若△AOM的面积等于12,求l的函数解析式.
分析 (1)将y=-2代入y=-2中求出x的值,即可得出点B的坐标,结合点B的坐标利用反比例函数图象上点的坐标特征即可求出双曲线的解析式;
(2)设过原点O的另一条直线l的解析式为y=mx,由点B的坐标可得出点A的坐标,根据△AOM的面积等于12结合三角形的面积公式可求出点M的坐标,由点A、M的坐标利用待定系数法即可求出直线AM的解析式,联立直线AM与双曲线的解析式得出关于x、y的方程组,解方程组即可求出点P的坐标,再将点P坐标带入y=mx中求出m即可得出结论.
解答 解:(1)将y=-2代入$y=\frac{1}{2}x$中,
得:-2=$\frac{1}{2}$x,解得:x=-4,
∴点B(-4,-2),
∴k=-4×(-2)=8,
∴双曲线的解析式为y=$\frac{8}{x}$.
(2)依照题意画出图形,如图所示.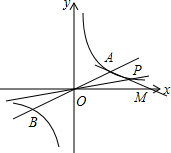
设过原点O的另一条直线l的解析式为y=mx,
∵点B(-4,-2),
∴点A(4,2).
∵S△AOM=$\frac{1}{2}$OM•yA=12,
∴OM=12,
∴点M(12,0).
设直线AM的解析式为y=ax+b,
则有$\left\{\begin{array}{l}{2=4a+b}\\{0=12a+b}\end{array}\right.$,解得:$\left\{\begin{array}{l}{a=-\frac{1}{4}}\\{b=3}\end{array}\right.$,
∴直线AM的解析式为y=-$\frac{1}{4}$x+3.
联立直线AM和双曲线解析式得:$\left\{\begin{array}{l}y=\frac{8}{x}\\ y=-\frac{1}{4}x+3\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=4}\\{y=2}\end{array}\right.$(舍去)或$\left\{\begin{array}{l}{x=8}\\{y=1}\end{array}\right.$,
∴点P(8,1).
将点P(8,1)代入y=mx中,
得:1=8m,解得:m=$\frac{1}{8}$,
∴直线l的函数解析式为y=$\frac{1}{8}$x.
点评 本题考查了反比例函数图象上点的坐标特征.反比例函数与一次函数的交点问题、待定系数法求函数解析式以及三角形的面积公式,解题的关键是:(1)求出点B的坐标;(2)求出点P的坐标.本题属于中档题,难度不大,但解题过程较繁琐,解决该题型题目时,联立两函数解析式成方程组,通过求方程组找出交点坐标是关键.

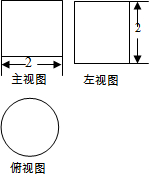 如图是某几何体的三视图,下列判断正确的是( )
如图是某几何体的三视图,下列判断正确的是( )| A. | 几何体是圆柱体,高为2 | B. | 几何体是圆锥体,高为2 | ||
| C. | 几何体是圆柱体,半径为2 | D. | 几何体是圆锥体,直径为2 |
| A. |  | B. |  | C. |  | D. |  |
 反比例函数y=$\frac{k}{x}$在第一象限的图象如图,请写出一个满足条件的k值,k=3.
反比例函数y=$\frac{k}{x}$在第一象限的图象如图,请写出一个满足条件的k值,k=3.