题目内容
如图，两艘军同时从某军港口出发执行任务，甲舰以30海里/时的速度向西北方向航行，乙舰以40海里/时的速度向西南方向航行，1.5小时后两舰相距多远？考点：勾股定理的应用,方向角
专题：
分析：先求出OA及OB的长，再根据勾股定理求出AB的长即可．
解答：解：∵舰以30海里/时的速度向西北方向航行，乙舰以40海里/时的速度向西南方向航行，
∴∠AOB=90°，OA=30×1.5=45，OB=40×1.5=60，
∴AB=
=
=75（海里）．
答：1.5小时后两舰相距75海里．
∴∠AOB=90°，OA=30×1.5=45，OB=40×1.5=60，
∴AB=
| OA2+OB2 |
| 452+602 |
答：1.5小时后两舰相距75海里．
点评：本题考查的是勾股定理的应用，在应用勾股定理解决实际问题时勾股定理与方程的结合是解决实际问题常用的方法，关键是从题中抽象出勾股定理这一数学模型，画出准确的示意图．领会数形结合的思想的应用．
练习册系列答案
相关题目
下列四个图案中是轴对称图形的有（ ）
| A、1个 | B、2个 | C、3个 | D、4个 |
已知二次函数y=ax2+bx-1图象的开口向下，对称轴在y轴右侧，则直线y=ax+b的图象经过的象限是（ ）
| A、第一、二、三象限 |
| B、第一、二、四象限 |
| C、第一、三、四象限 |
| D、第二、三、四象限 |
矩形ABCD中，E为AB中点、F为CD中点，G为CB延长线上一点，连接GE并延长交AC与点H，连接GF，求证：∠HFE=∠EFG．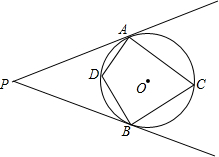
如图，PA，PB是⊙O的切线，A，B为切点，C为优弧AB上一点，D为劣弧AB上一点．求证：