Question

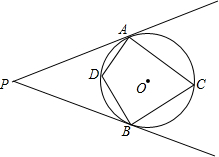如图，PA，PB是⊙O的切线，A，B为切点，C为优弧AB上一点，D为劣弧AB上一点．求证：
（1）∠D=90°+

1

2

∠P；
（2）∠C=90°-

1

2

∠P．

Answer 1

考点：切线的性质

专题：证明题

分析：由PA，PB是⊙O的切线，根据切线的性质得∠OAP=∠OBP=90°，则利用四边形内角和得到∠AOB=180°-∠P，再根据圆周角定理得∠C=

1

2

∠AOB，所以∠C=90°-

1

2

∠P；然后利用圆内接四边形的性质证明∠ADB=90°+

1

2

∠P．

解答：证明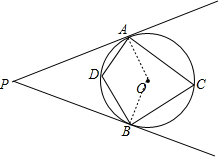：连结OA、OB，如图，
∵PA，PB是⊙O的切线，
∴OA⊥PA，OB⊥PB，
∴∠OAP=∠OBP=90°，
∴∠AOB+∠P=180°，
即∠AOB=180°-∠P，
∵∠C=

1

2

∠AOB，
∴∠C=

1

2

（180°-∠P）=90°-

1

2

∠P；
∵∠ADB+∠C=180°，
∴∠ADB=180°-∠C=180°-（90°-

1

2

∠P）=90°+

1

2

∠P．

点评：本题考查了切线的性质：圆的切线垂直于经过切点的半径．也考查了圆内接四边形的性质．