题目内容
5.数学活动课上,王老师说:“$\sqrt{6}$是无理数,无理数就是无限不循环小数,同学们,你能把$\sqrt{6}$的小数部分全部写出来吗?”大家议论纷纷,小明同学说:“要把它的小数部分全部写出来是非常难的,但我们可以用$\sqrt{6}$-2表示它的小数部分.”王老师说:“小明同学的说法是正确的,因为$\sqrt{6}$的整数部分是2,将这个数减去其整数部分,差就是小数部分,”请你解答:已知7+$\sqrt{13}$=x+y,其中x是一个整数,且0<y<1,求出3x+($\sqrt{13}$-y)的值.分析 先估算$\sqrt{13}$的范围,进一步确定7+$\sqrt{13}$的范围,即可求出x,y的值,即可解答.
解答 解:∵3<$\sqrt{13}$<4,
∴10<7+$\sqrt{13}$<11,
∵7+$\sqrt{13}$=x+y,且x是一个整数,0<y<1,
∴x=10,y=7+$\sqrt{13}$-10=$\sqrt{13}$-3,
∴3x+($\sqrt{13}$-y)=3×10+[$\sqrt{13}$-($\sqrt{13}$-3)]=33.
点评 本题考查了估算无理数的大小,解决本题的关键是估算$\sqrt{13}$的范围.

练习册系列答案
相关题目
16.下列属于最简二次根式的是( )
| A. | $\sqrt{21}$ | B. | 2$\sqrt{12}$ | C. | $\sqrt{18}$ | D. | $\sqrt{20}$ |
13.2是-2的( )
| A. | 倒数 | B. | 算术平方根 | C. | 绝对值 | D. | 平方根 |
20.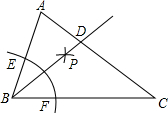 如图,已知△ABC,∠ABC=2∠C,以B为圆心任意长为半径作弧,交BA、BC于点E、F,分别以E、F为圆心,以大于$\frac{1}{2}$EF的长为半径作弧,两弧交于点P,作射线BP交AC于点,则下列说法不正确的是( )
如图,已知△ABC,∠ABC=2∠C,以B为圆心任意长为半径作弧,交BA、BC于点E、F,分别以E、F为圆心,以大于$\frac{1}{2}$EF的长为半径作弧,两弧交于点P,作射线BP交AC于点,则下列说法不正确的是( )
 如图,已知△ABC,∠ABC=2∠C,以B为圆心任意长为半径作弧,交BA、BC于点E、F,分别以E、F为圆心,以大于$\frac{1}{2}$EF的长为半径作弧,两弧交于点P,作射线BP交AC于点,则下列说法不正确的是( )
如图,已知△ABC,∠ABC=2∠C,以B为圆心任意长为半径作弧,交BA、BC于点E、F,分别以E、F为圆心,以大于$\frac{1}{2}$EF的长为半径作弧,两弧交于点P,作射线BP交AC于点,则下列说法不正确的是( )| A. | ∠ADB=∠ABC | B. | AB=BD | C. | AC=AD+BD | D. | ∠ABD=∠BCD |
10.若(x+3)(2x-n)=2x2+mx-15,则m、n的值分别是( )
| A. | m=-1.n=5 | B. | m=1,n=5 | C. | m=-1,n=-5 | D. | m=1,n=-5 |
14.如果每盒钢笔有10支,售价25元,那么购买钢笔的总钱数y(元)与支数x之间的关系式为( )
| A. | y=10x | B. | y=25x | C. | y=$\frac{2}{5}$x | D. | y=$\frac{5}{2}$x |
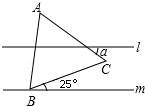 已知:如图,l∥m,等边△ABC的顶点B在直线m上,边BC与直线m所夹锐角为25°,则∠α的度数为35°.
已知:如图,l∥m,等边△ABC的顶点B在直线m上,边BC与直线m所夹锐角为25°,则∠α的度数为35°.