题目内容
3．已知抛物线y=ax2的开口向下，且|a|=3，则a=-3．分析 由抛物线y=ax2的开口向下，得出a＜0，再由|a|=3，a=±3，由此得出答案即可．
解答 解：∵抛物线y=ax2的开口向下，
∴a＜0，
∵|a|=3，
∴a=±3，
∴a=-3．
故答案为：-3．
点评 此题考查二次函数的性质，绝对值的意义，利用抛物线开口向下得出a＜0，是解决问题的关键．
练习册系列答案
津桥教育计算小状元系列答案
相关题目
15．
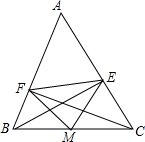如图，在△ABC中，CF⊥AB于点F，BE⊥AC于点E，M为BC的中点，EF=5，BC=8，则△EFM的周长及图中的等腰三角形个数分别是（ ）
如图，在△ABC中，CF⊥AB于点F，BE⊥AC于点E，M为BC的中点，EF=5，BC=8，则△EFM的周长及图中的等腰三角形个数分别是（ ）| A． | 21、2 | B． | 18、3 | C． | 13、4 | D． | 13、5 |
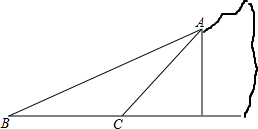因山体滑坡，需将一段50米长的滑坡体清除，滑坡体横截面是如图所示的△ABC．测得堡坎坡面AC的坡度是1：1，滑坡体坡面AB的坡角是30°，滑坡体底宽BC=13米．