题目内容
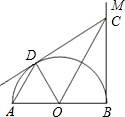 如图,AB是半圆(圆心为O)的直径,OD是半径,BM切半圆于B,OC与弦AD平行且交BM于C.
如图,AB是半圆(圆心为O)的直径,OD是半径,BM切半圆于B,OC与弦AD平行且交BM于C.(1)求证:CD是半圆的切线;
(2)若AB长为4,点D在半圆上运动,设AD长为x,点A到直线CD的距离为y,试求出y与x之间的函数关系式,并写出自变量x的取值范围.
考点:切线的判定,相似三角形的判定与性质
专题:证明题
分析:(1)根据切线的性质,由BM切半圆于B得∠OBC=90°,再根据圆周角定理得∠ADB=90°,即AD⊥BD,而OC∥AD,则OC⊥BD,于是可判断OC垂直平分BD,得到CD=CB,所以∠3=∠4,易得∠2+∠4=∠1+∠3=90°,即∠ODC=90°,然后根据切线得判定定理得到CD是半圆的切线;
(2)作AH⊥CD于H,如图,则AH=y,证明Rt△ABD∽Rt△ADH,利用相似比得x:y=4:x,则y=
x2(0<x<4).
(2)作AH⊥CD于H,如图,则AH=y,证明Rt△ABD∽Rt△ADH,利用相似比得x:y=4:x,则y=
| 1 |
| 4 |
解答:(1)证明:∵BM切半圆于B,
∴OB⊥BM,
∴∠OBC=90°,
∵AB是半圆(圆心为O)的直径,
∴∠ADB=90°,
∴AD⊥BD,
∵OC∥AD,
∴OC⊥BD,
∴OC平分BD,即OC垂直平分BD,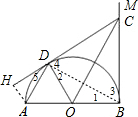
∴CD=CB,
∴∠3=∠4,
而∠1=∠2,
∴∠2+∠4=∠1+∠3=90°,即∠ODC=90°,
∴OD⊥DC,
∴CD是半圆的切线;
(2)解:作AH⊥CD于H,如图,则AH=y,
∵OD⊥CD,
∴∠5+∠ADO=90°,
而∠2+∠ADO=90°,∠1=∠2,
∴∠1=∠5,
∴Rt△ABD∽Rt△ADH,
∴AD:AH=AB:AD,即x:y=4:x,
∴y=
x2(0<x<4).
∴OB⊥BM,
∴∠OBC=90°,
∵AB是半圆(圆心为O)的直径,
∴∠ADB=90°,
∴AD⊥BD,
∵OC∥AD,
∴OC⊥BD,
∴OC平分BD,即OC垂直平分BD,

∴CD=CB,
∴∠3=∠4,
而∠1=∠2,
∴∠2+∠4=∠1+∠3=90°,即∠ODC=90°,
∴OD⊥DC,
∴CD是半圆的切线;
(2)解:作AH⊥CD于H,如图,则AH=y,
∵OD⊥CD,
∴∠5+∠ADO=90°,
而∠2+∠ADO=90°,∠1=∠2,
∴∠1=∠5,
∴Rt△ABD∽Rt△ADH,
∴AD:AH=AB:AD,即x:y=4:x,
∴y=
| 1 |
| 4 |
点评:本题考查了切线的判定:经过半径的外端且垂直于这条半径的直线是圆的切线.当已知条件中未明确指出直线和圆是否有公共点时,常过圆心作该直线的垂线段,证明该线段的长等于半径;当已知条件中明确指出直线与圆有公共点时,常连接过该公共点的半径,证明该半径垂直于这条直线.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
若x=2是关于x的方程x2-
ax+a2=0的一个根,则a的值为( )
| 5 |
| 2 |
| A、1或4 | B、-1或-4 |
| C、-1或4 | D、1或-4 |
-
的倒数是( )
| 1 |
| 2 |
| A、-2 | ||
| B、2 | ||
C、-
| ||
D、
|
 如图,已知在△ABC中,DE是AB的垂直平分线,AE=3cm,△BCD的周长为10cm,那么△ABC的周长为
如图,已知在△ABC中,DE是AB的垂直平分线,AE=3cm,△BCD的周长为10cm,那么△ABC的周长为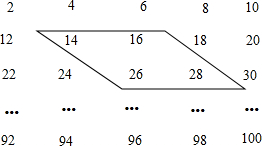 下列数阵是由50个偶数排成的.
下列数阵是由50个偶数排成的. 如图,小林种了一株高40cm的树苗,这株树苗平均每周长高5cm,几周后这株树苗的高超过1米?
如图,小林种了一株高40cm的树苗,这株树苗平均每周长高5cm,几周后这株树苗的高超过1米?