题目内容
 如图,在△ABC中,AD是BC边上的高,将△ABD沿AD折叠得到△AED,点E落在CD上,∠B=50°,∠C=30°.
如图,在△ABC中,AD是BC边上的高,将△ABD沿AD折叠得到△AED,点E落在CD上,∠B=50°,∠C=30°.(1)填空:∠BAD=
(2)求∠CAE的度数.
考点:三角形内角和定理,三角形的外角性质,翻折变换(折叠问题)
专题:
分析:(1)直接根据三角形内角和定理求出∠BAD的度数;
(2)先根据图形折叠的性质求出∠AED的度数,再由三角形外角的性质即可得出结论.
(2)先根据图形折叠的性质求出∠AED的度数,再由三角形外角的性质即可得出结论.
解答:解:(1)∵AD是BC边上的高,∠B=50°,
∴∠BAD=180°-90°-50°=40°.
故答案为:40;
(2)解法一:∵△AED是由△ABD折叠得到,
∴∠AED=∠B=50°,
∵∠AED是△ACE的外角,
∴∠AED=∠CAE+∠C,
∴∠CAE=∠AED-∠C=50°-30°=20°.
解法二:
∵△AED是由△ABD折叠得到,
∴∠EAD=∠BAD=40°,
∴∠BAE=80°,
∴∠CAE=180°-∠B-∠C-∠BAE=180°-50°-30°-80°=20°.
∴∠BAD=180°-90°-50°=40°.
故答案为:40;
(2)解法一:∵△AED是由△ABD折叠得到,
∴∠AED=∠B=50°,
∵∠AED是△ACE的外角,
∴∠AED=∠CAE+∠C,
∴∠CAE=∠AED-∠C=50°-30°=20°.
解法二:
∵△AED是由△ABD折叠得到,
∴∠EAD=∠BAD=40°,
∴∠BAE=80°,
∴∠CAE=180°-∠B-∠C-∠BAE=180°-50°-30°-80°=20°.
点评:本题考查的是三角形内角和定理,熟知三角形的内角和等于180°是解答此题的关键.

练习册系列答案
相关题目
 如图,?ABCD中,∠B=70°,点E是BC的中点,点F在AB上,且BF=BE,过点F作FG⊥CD于点G,则∠EGC的度数为( )
如图,?ABCD中,∠B=70°,点E是BC的中点,点F在AB上,且BF=BE,过点F作FG⊥CD于点G,则∠EGC的度数为( )| A、35° | B、45° |
| C、30° | D、55° |
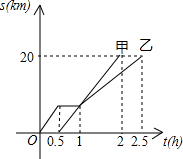 甲、乙两同学骑自行车从A地沿同一条路到B地,已知如图,甲做匀速运动,乙比甲先出发,他们离出发地距离s(km)和骑车行驶时间t(h) 之间的函数关系如图,给出下列说法:
甲、乙两同学骑自行车从A地沿同一条路到B地,已知如图,甲做匀速运动,乙比甲先出发,他们离出发地距离s(km)和骑车行驶时间t(h) 之间的函数关系如图,给出下列说法: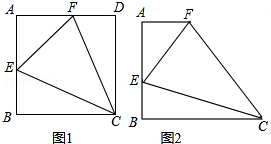 如图1,在正方形ABCD中,∠ECF的两边分别交边AB、AD于点E、F,且∠ECF=45°.
如图1,在正方形ABCD中,∠ECF的两边分别交边AB、AD于点E、F,且∠ECF=45°.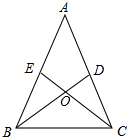 已知:如图,在锐角三角形ABC中,AB=AC,两条高BD与CE相交于点O,求证:OB=OC.
已知:如图,在锐角三角形ABC中,AB=AC,两条高BD与CE相交于点O,求证:OB=OC.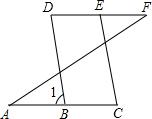 如图,已知:∠A=∠F,∠C=∠D,求证:BD∥EC,下面是不完整的说明过程,请将过程及其依据补充完整.
如图,已知:∠A=∠F,∠C=∠D,求证:BD∥EC,下面是不完整的说明过程,请将过程及其依据补充完整.