题目内容
2．方程组$\left\{\begin{array}{l}{x+y=5}\\{x-2y=2}\end{array}\right.$的解是（ ）| A． | $\left\{\begin{array}{l}{x=1}\\{y=4}\end{array}\right.$ | B． | $\left\{\begin{array}{l}{x=3}\\{y=2}\end{array}\right.$ | C． | $\left\{\begin{array}{l}{x=8}\\{y=-3}\end{array}\right.$ | D． | $\left\{\begin{array}{l}{x=4}\\{y=1}\end{array}\right.$ |
分析 方程组利用加减消元法求出解即可．
解答 解：$\left\{\begin{array}{l}{x+y=5①}\\{x-2y=2②}\end{array}\right.$，
①-②得：3y=3，即y=1，
把y=1代入①得：x=4，
则方程组的解为$\left\{\begin{array}{l}{x=4}\\{y=1}\end{array}\right.$，
故选D．
点评 此题考查了解二元一次方程组，利用了消元的思想，消元的方法有：代入消元法与加减消元法．
练习册系列答案
相关题目
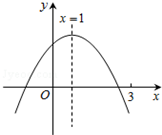二次函数y=ax2+bx+c（a≠0）图象如图，下列结论：①abc＞0；②2a+b=0；③当m≠1时，a+b＞am2+bm；④a-b+c＞0；⑤若ax12+bx1=ax22+bx2，且x1≠x2，x1+x2=2．其中正确的有②③⑤．
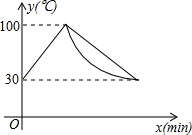饮水机接通电源就进入自动程序，若在水温为30℃时，接通电源后，水温y（℃）和时间x（min）的关系如图．开机加热时每分钟上升10℃，加热到100℃，饮水机关机停止加热，水温开始下降，下降时水温与开机后的时间成反比例关系．当水温降至30℃，饮水机自动开机，重复上述自动程序．若上午7：20开机，则8：00时能否喝到超过50℃的水？说明理由．
11．祁中初三66班学生毕业时，每个同学都要给其他同学写一份毕业留言作为纪念，全班学生共写了930份留言．如果全班有x名学生，根据题意，列出方程为（ ）
| A． | $\frac{x（x-1）}{2}$=930 | B． | $\frac{x（x+1）}{2}$=930 | C． | x（x+1）=930 | D． | x（x-1）=930 |