题目内容
4.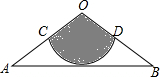 如图,从一张腰长为60cm,顶角为120°的等腰三角形铁皮OAB中剪出一个最大的扇形OCD,用此剪下的扇形铁皮围成一个圆锥的侧面(不计损耗),则该圆锥的高为20$\sqrt{2}$cm.
如图,从一张腰长为60cm,顶角为120°的等腰三角形铁皮OAB中剪出一个最大的扇形OCD,用此剪下的扇形铁皮围成一个圆锥的侧面(不计损耗),则该圆锥的高为20$\sqrt{2}$cm.
分析 根据等腰三角形的性质得到OE的长,再利用弧长公式计算出弧CD的长,设圆锥的底面圆的半径为r,根据圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长得到r,然后利用勾股定理计算出圆锥的高.
解答  解:过O作OE⊥AB于E,∵OA=OB=60cm,∠AOB=120°,
解:过O作OE⊥AB于E,∵OA=OB=60cm,∠AOB=120°,
∴∠A=∠B=30°,
∴OE=$\frac{1}{2}$OA=30cm,
∴弧CD的长=$\frac{120π×30}{180}$=20π,
设圆锥的底面圆的半径为r,则2πr=20π,解得r=10,
∴圆锥的高=$\sqrt{3{0}^{2}-1{0}^{2}}$=20$\sqrt{2}$.
故答案为:20$\sqrt{2}$.
点评 本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.

练习册系列答案
相关题目
13.若a,b,c为三角形的三边,则下列各组数据中,不能组成直角三角形的是( )
| A. | a=14,b=48,c=49 | B. | a=3,b=5,c=4 | C. | a=9,b=40,c=41 | D. | a=8,b=15,c=17 |

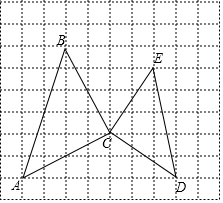 在如图10×9的网格图中,△ABC和△CDE都是等腰直角三角形,其顶点都在格点上,若点A、C的坐标分别为(-5,-2)和(-1,0).
在如图10×9的网格图中,△ABC和△CDE都是等腰直角三角形,其顶点都在格点上,若点A、C的坐标分别为(-5,-2)和(-1,0).
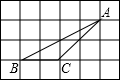 如图,△ABC的顶点都是正方形网格的格点,求∠BAC的三个三角函数值.
如图,△ABC的顶点都是正方形网格的格点,求∠BAC的三个三角函数值.