题目内容
用配方法求抛物线y=-x2-2x+3的顶点坐标．
解：y=-x2-2x+3
=-（x2+2x）+3
=-（x2+2x+1）+4
=-（x+1）2+4
所以抛物线顶点坐标为（-1，4）．
分析：这个函数的二次项系数是-1，配方法变形成y=（x+h）2+k的形式，配方的方法是把二次项，一次项先分为一组，提出一次项系数-1，加上一次项系数的一半，就可以变形成顶点式的形式．
点评：本题主要考查了配方法确定二次函数的顶点及对称轴，在配方的过程中注意要保持式子的值不变．
=-（x2+2x）+3
=-（x2+2x+1）+4
=-（x+1）2+4
所以抛物线顶点坐标为（-1，4）．
分析：这个函数的二次项系数是-1，配方法变形成y=（x+h）2+k的形式，配方的方法是把二次项，一次项先分为一组，提出一次项系数-1，加上一次项系数的一半，就可以变形成顶点式的形式．
点评：本题主要考查了配方法确定二次函数的顶点及对称轴，在配方的过程中注意要保持式子的值不变．
练习册系列答案
新课标阶梯阅读训练系列答案
口算心算速算应用题系列答案
同步拓展阅读系列答案
相关题目
与x轴的另一个交点为E．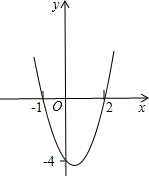
已知二次函数y=ax2+bx+c（a≠0）的图象如图；