题目内容
已知抛物线y=
x2+x-
(1)用配方法求抛物线的顶点坐标.
(2)x取何值时,y随x的增大而减大.
(3)若抛物线与x轴的两个交点为A、B,与y轴的交点为C,求S△ABC.
| 1 |
| 2 |
| 5 |
| 2 |
(1)用配方法求抛物线的顶点坐标.
(2)x取何值时,y随x的增大而减大.
(3)若抛物线与x轴的两个交点为A、B,与y轴的交点为C,求S△ABC.
分析:(1)利用完全平方式将
x2+x-
化为完全平方的形式;
(2)判断出函数的开口方向,找到函数的对称轴即可判断函数的增减性;
(3)令y=0,建立关于x的方程,求出x的值即为函数与x轴交点的横坐标,从而得到函数与x轴的两个交点,进而求出函数解析式.
| 1 |
| 2 |
| 5 |
| 2 |
(2)判断出函数的开口方向,找到函数的对称轴即可判断函数的增减性;
(3)令y=0,建立关于x的方程,求出x的值即为函数与x轴交点的横坐标,从而得到函数与x轴的两个交点,进而求出函数解析式.
解答:解:(1)∵y=
x2+x-
=
(x2+2x)-
=
(x2+2x+1-1)-
=
(x2+2x+1)-
-
=
(x+1)2-3,
∴抛物线的顶点坐标为(-1,-3).
(2)由于抛物线开口向上,对称轴为x=-1,
可见,当x<-1时,y随x的增大而减小.
(3)令y=0,
x2+x-
=0时,
解得x1=
-1,x2=-
-1,
∴AB=2
,
又∵C点坐标为(0,-
),
∴S△ABC=
×2
×
=
.
| 1 |
| 2 |
| 5 |
| 2 |
=
| 1 |
| 2 |
| 5 |
| 2 |
=
| 1 |
| 2 |
| 5 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
=
| 1 |
| 2 |
∴抛物线的顶点坐标为(-1,-3).
(2)由于抛物线开口向上,对称轴为x=-1,
可见,当x<-1时,y随x的增大而减小.
(3)令y=0,
| 1 |
| 2 |
| 5 |
| 2 |
解得x1=
| 6 |
| 6 |
∴AB=2
| 6 |
又∵C点坐标为(0,-
| 5 |
| 2 |
∴S△ABC=
| 1 |
| 2 |
| 6 |
| 5 |
| 2 |
5
| ||
| 2 |
点评:本题考查了二次函数的性质、抛物线与x轴的交点,熟悉函数与方程的关系是解题的关键.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
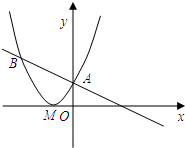 角形?若存在,求出点P的坐标;若不存在,请说明理由.
角形?若存在,求出点P的坐标;若不存在,请说明理由.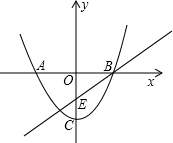 已知抛物线y=ax2+c与x轴交于A、B两点,与y轴交于C点,直线y=
已知抛物线y=ax2+c与x轴交于A、B两点,与y轴交于C点,直线y=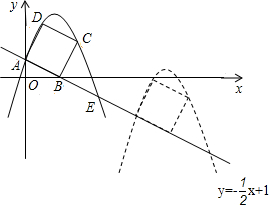
 如图,已知直线
如图,已知直线 +12x-19的顶点的横坐标是3,则a=________.
+12x-19的顶点的横坐标是3,则a=________.