题目内容
6.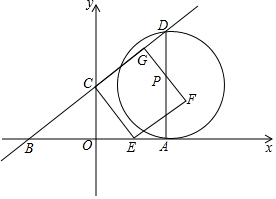 如图,在直角坐标系中,点A(12,0),点C在y轴正半轴上,点B在x轴的负半轴上,且$\frac{OC}{OB}$=$\frac{3}{4}$,过点C作CE⊥BC交x轴于点E,以CE为边在第一象限构造正方形CEFG,过点A作AD⊥x轴交直线BC于点D.记OC=3t,解答下列问题:
如图,在直角坐标系中,点A(12,0),点C在y轴正半轴上,点B在x轴的负半轴上,且$\frac{OC}{OB}$=$\frac{3}{4}$,过点C作CE⊥BC交x轴于点E,以CE为边在第一象限构造正方形CEFG,过点A作AD⊥x轴交直线BC于点D.记OC=3t,解答下列问题:(1)用关于t的代数式表示AD的长度;
(2)当点E在线段OA(不含端点)上时,记四边形AECD的面积为S,求S关于t的函数关系式,并写出自变量t的取值范围;
(3)以AD为直径作⊙P.
①当正方形CEFO的一边所在直线与⊙P相切时,求出所有满足条件的t的值;
②当点P在正方形CEFG内部且刚好落在对角线上时,直接写出t的值.
分析 (1)如图1中,由OC∥AD,可得$\frac{OC}{AD}$=$\frac{OB}{BA}$,即$\frac{3t}{AD}$=$\frac{4t}{4t+12}$,由此推出AD=3t+9.
(2)由△BOC∽△COE,可得OC2=BO•OE,推出EO=$\frac{9}{4}$t,由题意0<$\frac{9}{4}$t<12,推出0<t<$\frac{16}{3}$.构建S=S梯形AOCD-S△COE计算即可.
(3)①分三四种情形分别讨论,想办法构建方程解决问题.
②分两种情形构建一次函数解决问题.
解答 解:(1)如图1中,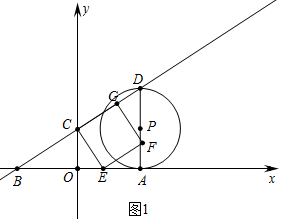
∵$\frac{OC}{OB}$=$\frac{3}{4}$,OC=3t,
∴OB=4t,
∵AD⊥AB,OC⊥AB,
∴OC∥AD,
∴$\frac{OC}{AD}$=$\frac{OB}{BA}$,
∴$\frac{3t}{AD}$=$\frac{4t}{4t+12}$,
∴AD=3t+9.
(2)如图1中,
∵CE⊥BC,
∴∠BCE=90°,
∴∠BCO+∠OCE=90°,∵∠BCO+∠CBO=90°,
∴∠OCE=∠CBO,∵∠BOC=∠EOC,
∴△BOC∽△COE,
∴OC2=BO•OE,
∴EO=$\frac{9}{4}$t,
由题意0<$\frac{9}{4}$t<12,
∴0<t<$\frac{16}{3}$.
∴S=S梯形AOCD-S△COE=$\frac{1}{2}$•(3t+3t+9)•12-$\frac{1}{2}$•$\frac{9}{4}$t•3t=-$\frac{27}{8}$t2+36t+54.(0<t<$\frac{16}{3}$).
(3)①a、如图2中,当直线GF与⊙P相切时,作PH⊥CD于H,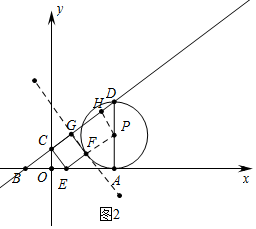
由△PHD∽△BOC可得,DH=$\frac{3}{10}$(3t+9),易知CE=$\frac{15}{4}$t,CD=15,
∴HC-CG=$\frac{1}{2}$(3t+9),
∴15-$\frac{3}{10}$(3t+9)-$\frac{15}{4}$t=$\frac{1}{2}$(3t+9),
解得t=$\frac{156}{123}$s.
当直线CE与⊙P相切时,CH=PA,则有15-$\frac{3}{10}$(3t+9)=$\frac{1}{2}$(3t+9),
解得t=$\frac{39}{12}$s,
b、如图3中,当⊙P与GF相切时,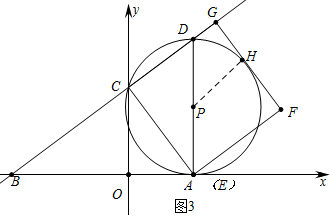
易知PH是梯形DGFA的中位线,
∴PH=$\frac{DG+AF}{2}$,
∴$\frac{3t+9}{2}$=$\frac{\frac{15}{4}t-15+\frac{15}{4}t}{2}$,
解得t=$\frac{11}{7}$s,
c、如图4中,当⊙P与EF相切时,设切点为H,连接HP,延长HP交CD于K.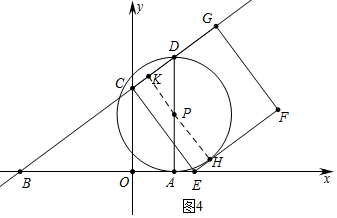
根据PA=PH,PH+PK=CE,
可得$\frac{3t+9}{2}$+$\frac{4}{5}$•$\frac{3t+9}{2}$=$\frac{15}{4}$t,
解得t=$\frac{162}{21}$s.
综上所述,当t=$\frac{156}{123}$s或$\frac{39}{12}$s或$\frac{11}{7}$s或$\frac{162}{21}$s时,⊙P与正方形CEFO的一边所在直线与⊙P相切.
②a、如图5中,当点P在对角线CF上时,作FH⊥OA于H.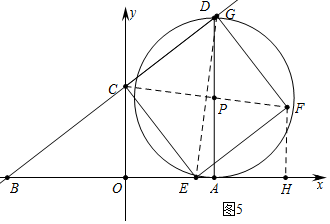
易证△EOC≌△FHE,
∴FH=OE=$\frac{9}{4}$t,EH=OC=3t,
∴F($\frac{21}{4}$t,$\frac{9}{4}$t),
∴直线CF的解析式为y=-$\frac{1}{7}$x+3t,
把P(12,$\frac{3t+9}{2}$)代入直线CF的解析式为y=-$\frac{1}{7}$x+3t,
得$\frac{3t+9}{2}$=-$\frac{12}{7}$+3t,
解得t=$\frac{87}{31}$s.
b、如图6中,当点P在对角线DE上时.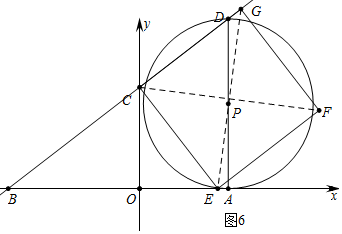
∵EG⊥CF,
∴直线EG的解析式为y=7x-$\frac{63}{4}$t,
把P(12,$\frac{3t+9}{2}$)代入直线EG的解析式为y=7x-$\frac{63}{4}$t,
得$\frac{3t+9}{2}$=84-$\frac{63}{4}$t,
解得t=$\frac{106}{23}$s.
综上所述,当t=$\frac{87}{31}$s或$\frac{106}{23}$s时,点P在正方形CEFG内部且刚好落在对角线上.
点评 本题考查圆综合题、正方形的性质、相似三角形的判定和性质、一次函数的性质、全等三角形的判定和性质、勾股定理、平行线分线段成比例定理、梯形中位线定理等知识,解题的关键是灵活运用所学知识解决问题,学会用分类讨论的思想思考问题,学会构建方程解或构建一次函数解决问题,属于中考压轴题.

 如图,直线l1∥l2,l3⊥l4,∠1=44°,那么∠2的度数46°.
如图,直线l1∥l2,l3⊥l4,∠1=44°,那么∠2的度数46°.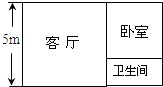 如图,有一长方形的仓库,一边长为5m,现要将它改建为简易住房,改建后的住房分为客厅、卧室和卫生间三部分,其中客厅和卧室都为正方形,且卧室的面积大于卫生间的面积,若改建后卫生间的面积为6m2,则长方形仓库另一边的长是8m.
如图,有一长方形的仓库,一边长为5m,现要将它改建为简易住房,改建后的住房分为客厅、卧室和卫生间三部分,其中客厅和卧室都为正方形,且卧室的面积大于卫生间的面积,若改建后卫生间的面积为6m2,则长方形仓库另一边的长是8m.