Question

12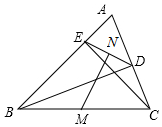．如图，已知在△ABC中，BD⊥AC于D，CE⊥AB于E，M，N分别是BC，DE的中点．
（1）求证：MN⊥DE；
（2）若BC=10，DE=6，求△MDE的面积．

Answer 1

分析 （1）连接ME、MD，由直角三角形的性质可求得DM=EN，则由等腰三角形的性质可证明MN⊥DE；
（2）由条件可求得MD、ND，在Rt△MND中可求得MN，则可求得△MDE的面积．

解答 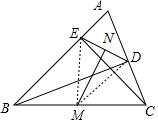（1）证明：
连接ME、MD，
∵BD⊥AC，
∴∠BDC=90°，
∵M是BC的中点，
∴DM=$\frac{1}{2}$BC，
同理可得EM=$\frac{1}{2}$BC，
∴DM=EM，
∵N是DE的中点，
∴MN⊥DE；
（2）解：
∵BC=10，ED=6，
∴DM=$\frac{1}{2}$BC=5，DN=$\frac{1}{2}$DE=3，
由（1）可知∠MND=90°，
∴MN=$\sqrt{M{D}^{2}-D{N}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4，
∴S_△MDE=$\frac{1}{2}$DE•MN=$\frac{1}{2}$×6×4=12

点评 本题主要考查直角三角形和等腰三角形的性质，利用直角三角形斜边上的中线等于斜边的一半求得DM=EM是解题的关键．