题目内容
3．
如图，BC是⊙O的直径，点D在⊙O上，AB是⊙O的切线，B为切点，连接CD并延长交AB于点A，若∠BOD=100°，则∠BAC的度数是（ ）| A． | 40° | B． | 45° | C． | 50° | D． | 80° |
分析 由切线的性质可知BC⊥BA，由圆周角定理可知∠C=50°，从而可求得∠A=40°．
解答 解：∵BA是圆O的切线，B为切点，
∴BC⊥BA．
∴∠CBA=90°．
∵∠BOD=100°，
∴∠C=50°．
∴∠A=90°-50°=40°．
故选：A．
点评 本题主要考查的是切线的性质和圆周角定理的应用，利用切线的性质和圆周角定理求得∠CBA=90°、∠C=50°是解题的关键．
练习册系列答案
名师指导期末冲刺卷系列答案
相关题目
14．下列说法正确的是（ ）
| A． | x3yz没有系数，次数是5 | B． | 3x-4y+6z2不是单项式，也不是整式 | ||
| C． | a+$\frac{a}{b}$是多项式 | D． | x2y+2是三次二项式 |
8．下面4个图形中，不是轴对称图形的是（ ）
| A． |  | B． |  | C． |  | D． |  |
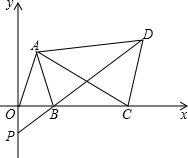如图，平面直角坐标系中，已知点A（1，3），B （2，0），C为x轴上点B右侧的动点，以AC为腰作等腰△ACD，使AD=AC，∠CAD=∠OAB，直线DB交y轴于点P．