题目内容
4.BD、CE是锐角△ABC的边AC、AB上的高,∠A=60°,则△ABC的面积和△AED的面积之比为( )| A. | 3:1 | B. | 9:5 | C. | 5:2 | D. | 4:1 |
分析 根据∠A的度数和BD⊥AC,CE⊥AB,即可求得AB=2AD,AC=2AE,进而可以求得△ABC与△ADE的面积的比值.
解答 解:∵∠A=60°,BD⊥AC,CE⊥AB,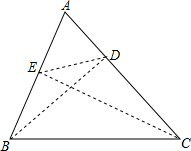
∴AB=2AD,AC=2AE,
∴△ADE的面积为$\frac{1}{2}$AD•AE•sinA,
△ABC的面积为$\frac{1}{2}$AB•AC•sinA,
∴△ADE的面积为△ABC面积的$\frac{1}{4}$,
即△ABC的面积和△AED的面积之比为:4:1.
故选D.
点评 本题主要考查了三角形面积的计算,特殊角的三角函数值在直角三角形中的运用,本题中求得AB=2AD,AC=2AE是解题的关键.

练习册系列答案
相关题目
14.下列一元一次方程中,解为x=1的是( )
| A. | 4x-1=3x | B. | 2x-2=3x+3 | C. | 3x+2=2x-1 | D. | 4x-3=3x-1 |
12.已知3m=a,81n=b,m、n为正整数,则33m+12n的值为( )
| A. | a3b3 | B. | 15ab | C. | 3a+12b | D. | a3+b3 |
19. 如图,矩形ABDC中,∠BAD的平分线交BC于E.若AB=4,AD=7,则S△DEC=( )
如图,矩形ABDC中,∠BAD的平分线交BC于E.若AB=4,AD=7,则S△DEC=( )
 如图,矩形ABDC中,∠BAD的平分线交BC于E.若AB=4,AD=7,则S△DEC=( )
如图,矩形ABDC中,∠BAD的平分线交BC于E.若AB=4,AD=7,则S△DEC=( )| A. | 6 | B. | 7 | C. | 8 | D. | 11 |
16.下列方程是关于x的一元二次方程的是( )
| A. | ax2+bx+c=0 | B. | |a|x2+bx+c=0 | C. | $\sqrt{a}$x2+bx+c=0 | D. | (a2+1)x2+bx+c=0 |
 在“文博会”期间,某公司展销如图所示的长方形工艺品.该工艺品长60cm,宽40cm,中间镶有宽度相同的三条丝绸花边.
在“文博会”期间,某公司展销如图所示的长方形工艺品.该工艺品长60cm,宽40cm,中间镶有宽度相同的三条丝绸花边.