题目内容
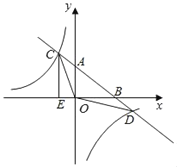
【题目】如图,一次函数y=ax+b的图象与反比例函数y=![]() 的图象交于C,D两点,与x,y轴交于B,A两点,CE⊥x轴于点E,且tan∠ABO=
的图象交于C,D两点,与x,y轴交于B,A两点,CE⊥x轴于点E,且tan∠ABO=![]() ,OB=4,OE=1.
,OB=4,OE=1.
(1)求一次函数的解析式和反比例函数的解析式
(2)求△OCD的面积;
(3)根据图象直接写出一次函数的值大于反比例函数的值时,自变量x的取值范围.
【答案】(1) y=﹣![]() x+2, y=﹣
x+2, y=﹣![]() ;(2) 6;(3) x<﹣1或0<x<5
;(2) 6;(3) x<﹣1或0<x<5
【解析】
(1)根据tan∠ABO=![]() ,OB=4,OE=1先把A、B、C点的坐标算出来,再用待定系数法即可把一次函数的解析式和反比例函数的解析式计算出来;
,OB=4,OE=1先把A、B、C点的坐标算出来,再用待定系数法即可把一次函数的解析式和反比例函数的解析式计算出来;
(2) 联立反比例函数的解析式和直线AB的解析式可得这两个函数图像的交点坐标,再根据面积公式即可求解;
(3)根据函数图像可以直接写出结果.
(1)∵OB=4,OE=1,
∴BE=1+4=5.
∵CE⊥x轴于点E,tan∠ABO=![]() =
=![]() =
=![]() ,
,
∴OA=2,CE=2.5.
∴点A的坐标为(0,2)、点B的坐标为C(4,0)、点C的坐标为(﹣1,2.5).
∵一次函数y=ax+b的图象与x,y轴交于B,A两点,
∴![]() ,
,
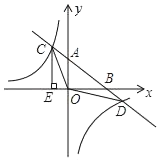
解得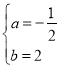 .
.
∴直线AB的解析式为y=﹣![]() x+2.
x+2.
∵反比例函数y=![]() 的图象过C,
的图象过C,
∴2.5=![]() ,
,
∴k=﹣2.5,
∴该反比例函数的解析式为y=﹣![]() ;
;
(2)联立反比例函数的解析式和直线AB的解析式可得 ,
,
解得点D的坐标为(5,﹣![]() ),
),
则△BOD的面积=4×![]() ×
×![]() =1,
=1,
△BOC的面积=4×![]() ×
×![]() =5,
=5,
∴△OCD的面积为1+5=6;
(3)由图象和点C、D的坐标得,一次函数的值大于反比例函数的值时x的取值范围:x<﹣1或0<x<5.

 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案【题目】昆明市某中学“综合实践活动”棋类社团前两次购买的两种材质的围棋采购如表(近期两种材质的围棋的售价一直不变):
塑料围棋 | 玻璃围棋 | 总价(元) | |
第一次(盒) |
|
|
|
第二次(盒) |
|
|
|
(1)若该社团计划再采购这两种材质的围棋各![]() 盒,则需要多少元;
盒,则需要多少元;
(2)若该社团准备购买这两种材质的围棋共![]() 盒,且要求塑料围棋的数量不多于玻璃围棋数量的
盒,且要求塑料围棋的数量不多于玻璃围棋数量的![]() 倍,请设计出最省钱的购买方案,并说明理由.
倍,请设计出最省钱的购买方案,并说明理由.