题目内容
【题目】昆明市某中学“综合实践活动”棋类社团前两次购买的两种材质的围棋采购如表(近期两种材质的围棋的售价一直不变):
塑料围棋 | 玻璃围棋 | 总价(元) | |
第一次(盒) |
|
|
|
第二次(盒) |
|
|
|
(1)若该社团计划再采购这两种材质的围棋各![]() 盒,则需要多少元;
盒,则需要多少元;
(2)若该社团准备购买这两种材质的围棋共![]() 盒,且要求塑料围棋的数量不多于玻璃围棋数量的
盒,且要求塑料围棋的数量不多于玻璃围棋数量的![]() 倍,请设计出最省钱的购买方案,并说明理由.
倍,请设计出最省钱的购买方案,并说明理由.
【答案】(1)采购这两种材质的围棋各![]() 盒需要
盒需要![]() 元;(2)最省钱的购买方案是购进塑料围棋
元;(2)最省钱的购买方案是购进塑料围棋![]() 盒,玻璃围棋
盒,玻璃围棋![]() 盒.
盒.
【解析】
(1)设一盒塑料围棋的售价是![]() 元,一盒玻璃围棋的售价是
元,一盒玻璃围棋的售价是![]() 元,依题意得
元,依题意得![]() ,解方程组可得;2)设购进玻璃围棋
,解方程组可得;2)设购进玻璃围棋![]() 盒,总费用为
盒,总费用为![]() 元,则
元,则![]() ,化简得
,化简得![]() ,求函数的最小值.
,求函数的最小值.
解:(1)设一盒塑料围棋的售价是![]() 元,一盒玻璃围棋的售价是
元,一盒玻璃围棋的售价是![]() 元,
元,
依题意得![]() ,解得
,解得![]() ,
,
![]() (元).
(元).
所以采购这两种材质的围棋各![]() 盒需要
盒需要![]() 元;
元;
(2)设购进玻璃围棋![]() 盒,总费用为
盒,总费用为![]() 元,
元,
则![]() ,化简得
,化简得![]() ,
,
所以当![]() 取最小值时,
取最小值时,![]() 有最小值,
有最小值,
因为![]() ,即
,即![]() ,
,
又![]() 为正整数,
为正整数,
所以当![]() 时,
时,![]() ,此时
,此时![]() (盒).
(盒).
所以最省钱的购买方案是购进塑料围棋![]() 盒,玻璃围棋
盒,玻璃围棋![]() 盒.
盒.

练习册系列答案
相关题目
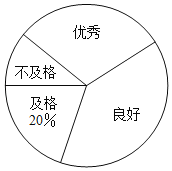
【题目】某校为了解八年级男生“立定跳远”成绩的情况,随机选取该年级部分男生进行测试,以下是根据测试成绩绘制的统计图表的一部分.
成绩等级 | 频数(人) | 频率 |
优秀 | 15 | 0.3 |
良好 | ||
及格 | ||
不及格 | 5 |
根据以上信息,解答下列问题
(1)被测试男生中,成绩等级为“优秀”的男生人数为 人,成绩等级为“及格”的男生人数占被测试男生总人数的百分比为 %;
(2)被测试男生的总人数为 人,成绩等级为“不及格”的男生人数占被测试男生总人数的百分比为 %;
(3)若该校八年级共有180名男生,根据调查结果,估计该校八年级男生成绩等级为“良好”的学生人数.