题目内容
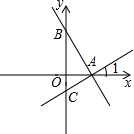 如图,在平面直角坐标系中,直线AB分别与x轴、y轴相交于A,B两点,OA、OB的长分别是方程x2-14x+48=0的两根,且OA<OB.
如图,在平面直角坐标系中,直线AB分别与x轴、y轴相交于A,B两点,OA、OB的长分别是方程x2-14x+48=0的两根,且OA<OB.(1)求点A,B的坐标.
(2)过点A作直线AC交y轴于点C,∠1是直线AC与x轴相交所成的锐角,sin∠1=
| 3 |
| 5 |
(3)若点M(m,m-5)在△AOC的内部,求m的取值范围.
考点:一次函数综合题
专题:压轴题
分析:(1)解关于x的一元二次方程,得到OA、OB的长度,然后写出坐标即可;
(2)根据锐角三角函数设OC=3k,AC=5k,再利用勾股定理列式求出k,从而得到OC的长度,再写出点C的坐标,然后利用待定系数法求一次函数解析式解答;
(3)根据点M在△AOC的内部列出不等式求解即可.
(2)根据锐角三角函数设OC=3k,AC=5k,再利用勾股定理列式求出k,从而得到OC的长度,再写出点C的坐标,然后利用待定系数法求一次函数解析式解答;
(3)根据点M在△AOC的内部列出不等式求解即可.
解答:解:(1)因式分解得,(x-6)(x-8)=0,
所以,x-6=0,x-8=0,
解得x1=6,x2=8,
∵OA<OB,
∴OA=6,OB=8,
∴点A(6,0),B(0,8);
(2)∵sin∠1=
,∠1=∠COA,
∴设OC=3k,AC=5k,
由勾股定理得,OC2+OA2=AC2,
即(3k)2+62=(5k)2,
解得k=
,
∴OC=3k=3×
=
,
∴点C(0,-
),
设直线AC的解析式为y=kx+b,
则
,
解得
,
所以,直线AC的解析式为y=
x-
;
(3)∵点M(m,m-5)在△AOC的内部,
∴
,
解不等式①得,m<5,
解不等式②得,m>2,
∴m的取值范围2<m<5.
所以,x-6=0,x-8=0,
解得x1=6,x2=8,
∵OA<OB,
∴OA=6,OB=8,
∴点A(6,0),B(0,8);
(2)∵sin∠1=
| 3 |
| 5 |
∴设OC=3k,AC=5k,
由勾股定理得,OC2+OA2=AC2,
即(3k)2+62=(5k)2,
解得k=
| 3 |
| 2 |
∴OC=3k=3×
| 3 |
| 2 |
| 9 |
| 2 |
∴点C(0,-
| 9 |
| 2 |
设直线AC的解析式为y=kx+b,
则
|
解得
|
所以,直线AC的解析式为y=
| 3 |
| 4 |
| 9 |
| 2 |
(3)∵点M(m,m-5)在△AOC的内部,
∴
|
解不等式①得,m<5,
解不等式②得,m>2,
∴m的取值范围2<m<5.
点评:本题是一次函数综合题,主要利用了一元二次方程的解法,待定系数法求一次函数解析式,锐角三角函数,勾股定理,一元一次不等式组的解法,(2)利用勾股定理列出方程然后求出OC的长度是解题的关键,(3)难点在于理解题意并列出不等式组.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
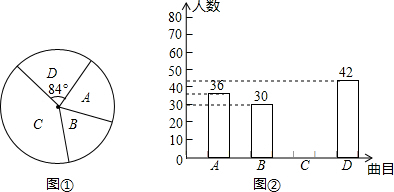
 为了解某校九年级学生体肓测试成绩情况,现从中随机抽取部分学生的体育成绩统计如下,其中如图扇形统计图中的圆心角α为36°.
为了解某校九年级学生体肓测试成绩情况,现从中随机抽取部分学生的体育成绩统计如下,其中如图扇形统计图中的圆心角α为36°.