Question

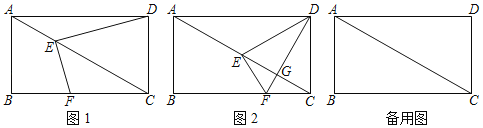
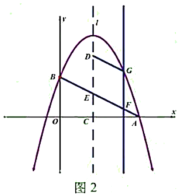
【题目】如图1，在平面直角坐标系中，抛物线与轴的一个交点为点，与轴的交点为点，抛物线的对称轴与轴交于点，与线段交于点，点是对称轴上一动点．

（1）点的坐标是________，点的坐标是________；

（2）是否存在点，使得和相似？若存在，请求出点的坐标，若不存在，请说明理由；

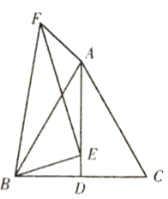
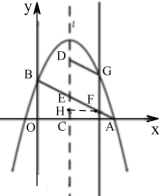
（3）如图2，抛物线的对称轴向右平移与线段交于点，与抛物线交于点，当四边形是平行四边形且周长最大时，求出点的横坐标．

Answer 1

【答案】（1），；（2）存在，或；（3）．

【解析】

（1）令x=0，求出y值可得B点坐标，令y=0，求出x值，根据点A在对称轴右侧可得点A坐标；

（2）根据抛物线解析式可求出对称轴为直线x=，根据A、B坐标可得直线AB的解析式，进而可求出点E坐标，即可求出CE的长，分、、三种情况，分别利用相似三角形的性质求出点D坐标即可得答案；

（3）过点做，设，，可用m表示出FG的长，利用勾股定理可求出AB的长，根据平移的性质可用m表示出FH的长，由平行线的性质可得，即可证明△BOA∽△EHF，根据相似三角形的性质可用m表示出EF的长，即可用m表示出平行四边形的周长，根据二次函数的性质即可得答案．

（1）令x=0得：y=3，

∴点B坐标为（0，3），

令y=0得：=0，

解得：x1=-1，x2=6，

∵点A在对称轴右侧，

∴点A坐标为（6，0），

故答案为：，

（2）存在，理由如下：

∵抛物线解析式为，

∴对称轴为直线，

设直线AB的解析式为y=kx+b，

∵A（6，0），B（0，3）

∴；

解得：，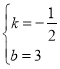

∴直线的解析式为

∴当时，，即E（，），

∴

①如图，当时，

∴，

∴，

∴，

∴，

∴，

∴．

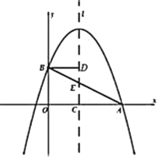
②当时，过点B作BF⊥l于F，

∵，，

∴，

∵对称轴为直线，

∴，EF=CF-CE=，

∵∠BDF+∠DBF=90°，∠EBF+∠DBF=90°，

∴∠BDF=∠EBF，

∵∠BFD=∠BFE，

∴，

∴，即，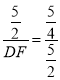

解得：DF=5，

∴CD=CF+DF=3+5=8，

∴．

③当时，不合题意舍去．

综上所述：或．

（3）过点做，设，，

∴，

∵抛物线的对称轴向右平移与线段交于点，

∴，

∵OA=6，OB=3，

∴，

∵，

∴，

∵，

∴△BOA∽△EHF，

∴，即，

∴，

∴，

∵，

∴时平行四边形周长最大，

∴的横坐标为．