题目内容
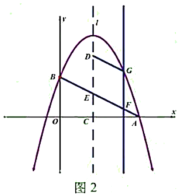
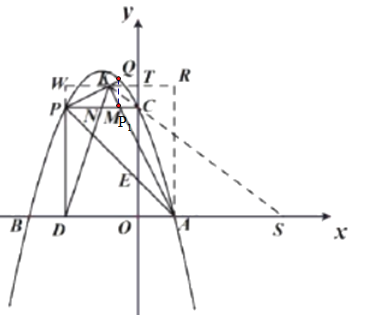
【题目】如图,在平面直角坐标系中,点![]() 为坐标原点,抛物线
为坐标原点,抛物线![]() 交
交![]() 轴于
轴于![]() 、
、![]() (
(![]() 左
左![]() 右)两点,交
右)两点,交![]() 轴于点
轴于点![]() ,
,![]() ,
,![]() .
.
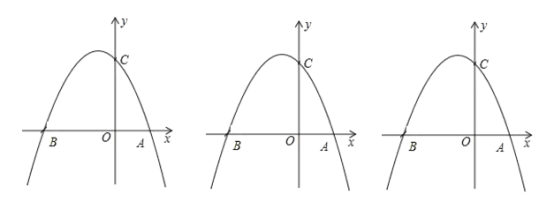
(1)求抛物线的解析式;
(2)点![]() 为第二象限抛物线上一点,连接
为第二象限抛物线上一点,连接![]() 、
、![]() ,
,![]() 交
交![]() 轴于点
轴于点![]() ,过点
,过点![]() 做
做![]() 轴的垂线,垂足为点
轴的垂线,垂足为点![]() ,过点
,过点![]() 做直线
做直线![]() 轴,在
轴,在![]() 轴上方直线
轴上方直线![]() 上取一点
上取一点![]() ,连接
,连接![]() ,使
,使![]() ,连接
,连接![]() 交
交![]() 轴于点
轴于点![]() ,当
,当![]() 时,求线段
时,求线段![]() 的长;
的长;
(3)在(2)的条件下,点![]() 为第二象限抛物线上的一点,连接
为第二象限抛物线上的一点,连接![]() ,过点
,过点![]() 做
做![]() 于点
于点![]() ,连接
,连接![]() ,线段
,线段![]() 、
、![]() 分别交线段
分别交线段![]() 于点
于点![]() 、
、![]() ,当
,当![]() 时,求
时,求![]() 的长度.
的长度.
【答案】(1)![]() ;(2)3;(3)
;(2)3;(3)![]()
【解析】
(1)令![]() ,求出y的值,即可求出C点坐标,根据
,求出y的值,即可求出C点坐标,根据![]() ,可求出B点坐标,把A、B点坐标代入解析式,即可求a、b的值,从而求出解析式;
,可求出B点坐标,把A、B点坐标代入解析式,即可求a、b的值,从而求出解析式;
(2)设![]() ,表示出
,表示出![]() ,
,![]() ,从而求出
,从而求出![]() ,从而推出
,从而推出![]() ,通过
,通过![]() ,列出关于m的方程,解方程求出m的值,即可求出PD的长;
,列出关于m的方程,解方程求出m的值,即可求出PD的长;
(3)过![]() 做
做![]() 交
交![]() 轴于
轴于![]() ,延长
,延长![]() 交
交![]() 延长线于
延长线于![]() ,过
,过![]() 做
做![]() ,连接
,连接![]() 并连延长交
并连延长交![]() 轴于
轴于![]() .证明
.证明![]() ,
,![]() ,通过相似三角形的性质可求出
,通过相似三角形的性质可求出![]() ,从而推出
,从而推出![]() ,设
,设![]() ,通过
,通过![]() ,可求出n的值,即可求出
,可求出n的值,即可求出![]() ,即可求出
,即可求出![]() 解析式为
解析式为![]() ,将
,将![]() 与抛物线解析式联立,解出x的值,从而求出Q的坐标,利用勾股定理可求
与抛物线解析式联立,解出x的值,从而求出Q的坐标,利用勾股定理可求![]() .
.
(1)![]() 对于
对于![]() 令
令![]() ,
,
∴![]() ,
,
∴![]() ,
,
![]()
∴![]() ,
,
![]()
将![]() 、
、![]() 代入
代入![]()
∴![]() ,解得
,解得![]()
∴抛物线的解析式为![]()
(2)如图;
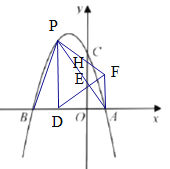
设![]()
![]() 轴
轴
∴![]() ,
,![]() ,
,
∴![]()
![]() ,
,
∴![]()
∴![]()
![]() ,
,
∴![]()
![]() ,
,
∴![]()
![]() ,
,
∴![]()
![]()
∴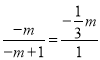
∴![]() ,
,
∴![]() ,
,
∴![]()
(3)过![]() 做
做![]() 交
交![]() 轴于
轴于![]() ,延长
,延长![]() 交
交![]() 延长线于
延长线于![]() ,过
,过![]() 做
做![]() ,连接
,连接![]() 并连延长交
并连延长交![]() 轴于
轴于![]() ,过Q点 作QP1⊥PC,交PC于点P1.
,过Q点 作QP1⊥PC,交PC于点P1.
![]() ,
,
又![]() ,
,
![]()
![]() ,
,![]()
![]()
![]() ,
,
![]() ,
,
![]()
![]()
设![]()
![]()
![]()
![]()
![]()
解得,![]() ,
,![]() (舍)
(舍)
![]() ,
,
∴![]() 解析式为
解析式为![]()
将![]() 与抛物线解析式联立
与抛物线解析式联立
![]()
解得,![]() (与
(与![]() 点重合舍掉),
点重合舍掉),![]()
![]()
∵![]() ,
,
∵![]() ,
,
∴PC∥x轴,
∵QP1⊥PC,
∴在Rt△PP1Q中,PP1= ![]() ,QP1=
,QP1= ![]()
![]() 利用勾股定理得:
利用勾股定理得:![]()

 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案【题目】黄山毛峰是中国十大名茶之一 ,产于安徽省黄山(徽州)一带,也称徽茶.有诗日:“未见黄山面,十里闻茶香”.某茶庄以![]() 元
元![]() 的价格收购一批毛峰,物价部门规定销售单价不低于成本且不得超过成本的
的价格收购一批毛峰,物价部门规定销售单价不低于成本且不得超过成本的![]() 倍,经试销过发现,日销量
倍,经试销过发现,日销量![]() 与销售单价
与销售单价![]() 的对应关系如下表:且
的对应关系如下表:且![]() 与
与![]() 满足初中所学某种函数关系.
满足初中所学某种函数关系.
|
|
|
|
| ··· |
|
|
|
|
| ··· |
(1)根据表格,求出![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)在销售过程中,每日还需支付其他费用![]() 元,当销售单价为多少时,该茶庄日利润最大?最大利润是多少元?
元,当销售单价为多少时,该茶庄日利润最大?最大利润是多少元?