题目内容
4．
如图，直线a、b被直线c所截，a∥b，∠2=∠3，若∠1=78°，则∠4等于（ ）| A． | 38° | B． | 39° | C． | 40° | D． | 41° |
分析 先根据平行线的性质，求得∠2+∠3的度数，再根据∠2=∠3，求得∠3的度数，最后根据平行线的性质，求得∠4即可．
解答 解∵a∥b，
∴∠2+∠3=∠1=78°，∠4=∠3，
∵∠2=∠3，
∴∠3=39°，
∴∠4=39°，
故选：B．
点评 本题主要考查了平行线的性质，解题时注意：两条平行线被第三条直线所截，内错角相等． 简单说成：两直线平行，内错角相等．
练习册系列答案
相关题目
15．一根蜡烛在凸透镜下成一实像，物距u，像距v和凸透镜的焦距f满足关系式$\frac{1}{u}$+$\frac{1}{v}$=$\frac{1}{f}$，f=6cm，v=8cm，则物距u的长为（ ）
| A． | 24cm | B． | 12cm | C． | $\frac{1}{24}$cm | D． | $\frac{1}{12}$cm |
12．
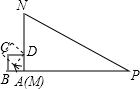如图，在Rt△MNP中，∠N=60°，MN=3，NP=6，正方形ABCD的边长为1，它的一边AD在MN上，且顶点A与M重合．现将正方形ABCD沿边MN→NP进行翻滚，直到正方形有一个顶点与P重合即停止滚动，正方形在整个翻滚过程中，点A所经过的路线与Rt△MNP的两边MN、NP所围成的图形的面积是（ ）
如图，在Rt△MNP中，∠N=60°，MN=3，NP=6，正方形ABCD的边长为1，它的一边AD在MN上，且顶点A与M重合．现将正方形ABCD沿边MN→NP进行翻滚，直到正方形有一个顶点与P重合即停止滚动，正方形在整个翻滚过程中，点A所经过的路线与Rt△MNP的两边MN、NP所围成的图形的面积是（ ）| A． | $\frac{7π}{3}$+2 | B． | 2π+2 | C． | $\frac{7π}{3}$ | D． | $\frac{4π}{3}$ |
19．在△ABC中，∠A、∠B、∠C的对边分别是a、b、c，下列说法错误的是（ ）
| A． | 若c2=b2-a2，那么△ABC是直角三角形且∠C=90° | |
| B． | 若∠C-∠B=∠A，那么△ABC是直角三角形 | |
| C． | 若（c+a）（c-a）=b2，那么△ABC是直角三角形 | |
| D． | 若∠A：∠B：∠C=5：2：3，那么△ABC是直角三角形 |
9．平面直角坐标系中，P（-2a-6，a-4）在第三象限，则a的取值范围是（ ）
| A． | a＞4 | B． | a≥-12 | C． | -3≤a＜4 | D． | -3＜a＜4 |
16．下列说法中正确的是（ ）
| A． | 0是最小的整数 | B． | 最大的负有理数是-1 | ||
| C． | 两个负数绝对值大的负数小 | D． | 有理数a的倒数是$\frac{1}{a}$ |