Question

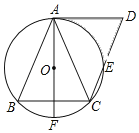
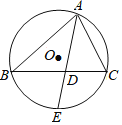
【题目】如图，已知△ABC内接于⊙O，AE平分∠BAC，交BC于D，交⊙O于E，若AB、AC的长是方程x2-ax+12=0的两实根，AD=2，则AE的长为（　　）

A.5B.6C.7D.8

Answer 1

【答案】B

【解析】

连接BE，如图，利用角平分线定义得到∠BAE=∠CAD，再根据圆周角定理得到∠E=∠C，则可判定△ABE∽△ADC，利用相似比得到ADAE=ABAC，然后根据根与系数的关系得到ABAC=12，从而可计算出AE的长．

解：连接BE，如图，

∵AE平分∠BAC，

∴∠BAE=∠CAD，

而∠E=∠C，

∴△ABE∽△ADC，

∴，即ADAE=ABAC，

∵AB、AC的长是方程x2-ax+12=0的两实根

∴ABAC=12，

而AD=2，

∴2AE=12，

∴AE=6．

故选B．