Question

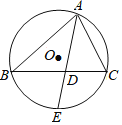
【题目】如图，AB＝AC，⊙O为△ABC的外接圆，AF为⊙O的直径，四边形ABCD是平行四边形．

（1）求证：AD是⊙O的切线；

（2）若∠BAC＝45°，AF＝2，求阴影部分的面积．

Answer 1

【答案】（1）证明见解析；（2）．

【解析】

（1）由题意根据垂径定理得到AF⊥BC，根据平行四边形的性质得到AD∥BC，求得AD⊥AF，于是得到AD是⊙O的切线；

（2）根据题意连接OC，OB，根据圆周角定理得到∠BOC=90°，根据勾股定理得到BC=，求得AD=BC=，连接OE，根据梯形和扇形的面积公式即可得到结论．

解：（1）∵AB＝AC，

∴，

∵AF为⊙O的直径，

∴AF⊥BC，

∵四边形ABCD是平行四边形，

∴AD∥BC，

∠AD⊥AF，

∴AD是⊙O的切线；

（2）连接OC，OB，

∵∠BAC＝45°，

∴∠BOC＝90°，

∵AF＝2，

∴OB＝OC＝1，

∴BC＝，

∵四边形ABCD是平行四边形，

∴AD＝BC＝，

连接OE，

∵AB∥BD，

∴∠ACE＝∠BAC＝45°，

∴∠AOE＝2∠ACE＝90°，

∵OA＝OE＝1，

∴阴影部分的面积＝S梯形AOED﹣S扇形AOE＝（1+）×1﹣＝．