题目内容
9.解方程:(1)x(x-2)=x-2;
(2)y(y-2)=1.
分析 (1)先把方程变形为x(x-2)-(x-2)=0,然后利用因式分解法解方程;
(2)先配方得到(y-1)2=2,然后利用直接开平方法解方程.
解答 解:(1)x(x-2)-(x-2)=0,
(x-2)(x-1)=0,
x-2=0或x-1=0,
所以x1=2,x2=1;
(2)y2-2y+1=2,
(y-1)2=2,
y-1=±$\sqrt{2}$,
所以y1=1+$\sqrt{2}$,x2=1-$\sqrt{2}$.
点评 本题考查了解一元二次方程-因式分解法:先把方程的右边化为0,再把左边通过因式分解化为两个一次因式的积的形式,那么这两个因式的值就都有可能为0,这就能得到两个一元一次方程的解,这样也就把原方程进行了降次,把解一元二次方程转化为解一元一次方程的问题了(数学转化思想).也考查了配方法解一元二次方程.

练习册系列答案
相关题目
19.若a+b<0,ab<0,则a,b两数应该是( )
| A. | a,b两数同正 | B. | a,b异号且负数的绝对值大 | ||
| C. | a,b两数同负 | D. | a,b异号且正数的绝对值大 |
18.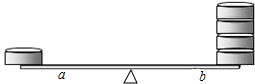 如图,用一根质地均匀的直尺和一些棋子做实验:在直尺的一端放一枚棋子.另一端放n枚棋子,移动质点的位置,使两边平衡,记录支点到两端的距离a,b,如下表:
如图,用一根质地均匀的直尺和一些棋子做实验:在直尺的一端放一枚棋子.另一端放n枚棋子,移动质点的位置,使两边平衡,记录支点到两端的距离a,b,如下表:
(1)根据统计记录,你发现的规律是a=nb;
(2)若直尺长60cm,直尺的一端放一枚棋子,另一端放9枚棋子,试用一元一次方程求出a,b的值.
 如图,用一根质地均匀的直尺和一些棋子做实验:在直尺的一端放一枚棋子.另一端放n枚棋子,移动质点的位置,使两边平衡,记录支点到两端的距离a,b,如下表:
如图,用一根质地均匀的直尺和一些棋子做实验:在直尺的一端放一枚棋子.另一端放n枚棋子,移动质点的位置,使两边平衡,记录支点到两端的距离a,b,如下表:| n(枚) | 1 | 2 | 3 | 4 | 5 |
| a/cm | 15 | 20 | 22.5 | 24 | 25 |
| b/cm | 15 | 10 | 7.5 | 6 | 5 |
(2)若直尺长60cm,直尺的一端放一枚棋子,另一端放9枚棋子,试用一元一次方程求出a,b的值.
 已知△ABC与△CDE按如图所示的方式放置,求证:∠BED>∠A.
已知△ABC与△CDE按如图所示的方式放置,求证:∠BED>∠A.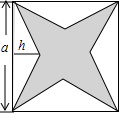 如图,一个正方形剪去四个相同的三角形,已知正方形的边长为a,三角形的高为h
如图,一个正方形剪去四个相同的三角形,已知正方形的边长为a,三角形的高为h