题目内容
5.先化简,再求值:$\frac{{a}^{3}}{{a}^{2}-6a+9}$÷(1+$\frac{3}{a-3}$),其中a=$\sqrt{2}$-1.分析 先根据分式混合运算的法则把原式进行化简,再把a的值代入进行计算即可.
解答 解:原式=$\frac{a({a}^{2}-9)}{{(a-3)}^{2}}$÷$\frac{a-3+3}{a-3}$
=$\frac{a(a+3)(a-3)}{{(a-3)}^{2}}$•$\frac{a-3}{a}$
=a+3.
当a=$\sqrt{2}$-1时,原式=$\sqrt{2}$-1+3=$\sqrt{2}$+2.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
相关题目
20.若关于x的一元二次方程2x2-x-n=0没有实数根,则二次函数y=2x2-x-n的图象的顶点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
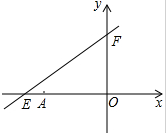 如图,直线y=kx+6与x轴、y轴分别交于点E,F,点E的坐标为(-8,0),点A的坐标为(-6,0)
如图,直线y=kx+6与x轴、y轴分别交于点E,F,点E的坐标为(-8,0),点A的坐标为(-6,0)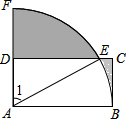 如图,矩形ABCD中,AB=2DA,以A为圆心,AB为半径的弧交DC于E,交AD的延长线于点F.
如图,矩形ABCD中,AB=2DA,以A为圆心,AB为半径的弧交DC于E,交AD的延长线于点F. 已知A(-2,0),B(4,0),C的坐标为(x,y),且S△ABC=12,|x|=3,求C点的坐标.
已知A(-2,0),B(4,0),C的坐标为(x,y),且S△ABC=12,|x|=3,求C点的坐标.