题目内容
1．在“母亲节”前夕，我市某校学生积极参与“关爱贫困母亲”的活动，他们购进一批单价为20元的“孝文化衫”在课余时间进行义卖，并将所得利润捐给贫困母亲．经试验发现，若每件按24元的价格销售时，每天能卖出36件；若每件按29元的价格销售时，每天能卖出21件．假定每天销售件数y（件）与销售价格x（元/件）满足一个以x为自变量的一次函数．（1）求y与x满足的函数关系式（不要求写出x的取值范围）；
（2）在不积压且不考虑其他因素的情况下，销售价格定为多少元时，才能使每天获得的利润P最大？
分析 （1）设y与x满足的函数关系式为：y=kx+b，由题意可列出k和b的二元一次方程组，解出k和b的值即可；
（2）根据题意：每天获得的利润为：P=（-3x+108）（x-20），转换为P=-3（x-28）2+192，于是求出每天获得的利润P最大时的销售价格．
解答 解：（1）设y与x满足的函数关系式为：y=kx+b．
由题意可得：
$\left\{\begin{array}{l}{24k+b=36}\\{29k+b=21}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{k=-3}\\{b=108}\end{array}\right.$，
∴y与x的函数关系式为：y=-3x+108；
（2）每天获得的利润为：
P=（-3x+108）（x-20）
=-3x2+168x-2160
=-3（x-28）2+192．
∵a=-3＜0，
∴当x=28时，利润最大，
∴当销售价定为28元时，每天获得的利润最大．
点评 本题主要考查二次函数的应用的知识点，解答本题的关键是熟练掌握二次函数的性质以及最值得求法，此题难度不大．
练习册系列答案
相关题目
如图，用边长为4和2的正方形拼成如图所示图形，则图中阴影部分的面积为$\frac{8}{3}$．
12．
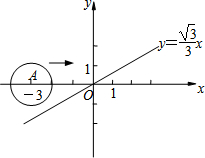如图，在平面直角坐标系中，x轴上一点A从点（-3，0）出发沿x轴向右平移，当以A为圆心，半径为1的圆与函数y=$\frac{\sqrt{3}}{3}$x的图象相切时，点A的坐标变为（ ）
如图，在平面直角坐标系中，x轴上一点A从点（-3，0）出发沿x轴向右平移，当以A为圆心，半径为1的圆与函数y=$\frac{\sqrt{3}}{3}$x的图象相切时，点A的坐标变为（ ）| A． | （-2，0） | B． | （-$\sqrt{3}$，0）或（$\sqrt{3}$，0） | C． | （-$\sqrt{3}$，0） | D． | （-2，0）或（2，0） |
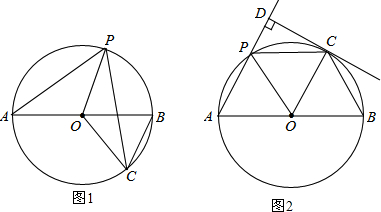
我们知道平行四边形有很多性质，现在如果我们把平行四边形沿着它的一条对角线翻折，会发现这其中还有更多的结论．