题目内容
3.解方程:(1)x2+4x-1=0
(2)(x+2)2-25=0.
分析 (1)把常数项-1移项后,应该在左右两边同时加上一次项系数4的一半的平方;
(2)把-25移项后,直接开平方即可.
解答 解:(1)移项得x2+4x=1,
配方得x2+4x+4=1+4,
即(x+2)2=5,
开方得x+2=±$\sqrt{5}$,
∴x1=$\sqrt{5}$-2,x2=-$\sqrt{5}$-2;
(2)移项得(x+2)2=25,
开方得x+2=±5,
∴x1=3,x2=-7.
点评 本题考查了解一元二次方程,配方法的一般步骤:
(1)把常数项移到等号的右边;
(2)把二次项的系数化为1;
(3)等式两边同时加上一次项系数一半的平方.
选择用配方法解一元二次方程时,最好使方程的二次项的系数为1,一次项的系数是2的倍数.

练习册系列答案
相关题目
15.下列计算正确的是( )
| A. | 6a3•6a4=6a7 | B. | (2+a)2=4+2a+a2 | C. | (3a3)2=6a6 | D. | (π-3.14)0=1 |
 如图,直线AB、CD相交于点O,OE平分∠BOD,∠AOC=72°,OF⊥CD.
如图,直线AB、CD相交于点O,OE平分∠BOD,∠AOC=72°,OF⊥CD.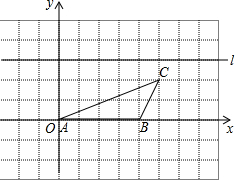 如图,在平面直角坐标系中,△ABC的边AB与x轴重合,点C的坐标是(5,2),在△ABC的上方有一直线l与x轴平行;
如图,在平面直角坐标系中,△ABC的边AB与x轴重合,点C的坐标是(5,2),在△ABC的上方有一直线l与x轴平行; 如图,AB为圆O的直径,弦CD⊥AB,垂足为点E,连结OC,若OC=5,CD=8,则AE的长是( )
如图,AB为圆O的直径,弦CD⊥AB,垂足为点E,连结OC,若OC=5,CD=8,则AE的长是( )