题目内容
9.定义:如图1,点M、N把线段AB分割成AM、MN、NB,若以AM、MN、NB为边的三角形是一个直角三角形,则称点M、N是线段AB的勾股分割点.(1)已知M、N把线段AB分割成AM、MN、NB,若AM=2,MN=4,BN=2$\sqrt{3}$,则点M、N是线段AB的勾股分割点;(填“是”或“不是”)
(2)已知点M、N是线段AB的勾股分割点,若AB=12,AM=5,求BN的长;
(3)如图2,P、Q是等腰Rt△ABC斜边AB的勾股分割点,PQ>AP,PQ>BQ,求∠PCQ的度数.
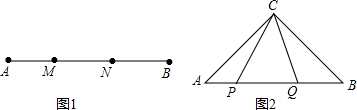
分析 (1)根据勾股定理逆定理即可判断.
(2)设BN=x,则MN=12-AM-BN=7-x,分三种情形①当AM为最大线段时,依题意AM2=MN2+BN2,②当MN为最大线段时,依题意MN2=AM2+NB2,③当BN为最大线段时,依题意BN2=AM2+MN2,分别列出方程即可解决问题.
(3)如图2中,把△CBQ绕点C顺时针旋转90°,得△ACR,连结RP,只要证明△PCR≌△PCQ得到
解答 解:(1)是.
理由:∵AM2+BN2=22+(2$\sqrt{3}$)2=16,MN2=42=16,
∴AM2+NB2=MN2,
∴AM、MN、NB为边的三角形是一个直角三角形.
故答案为是.
(2)设BN=x,则MN=12-AM-BN=7-x,
①当AM为最大线段时,依题意AM2=MN2+BN2,
即x2+(7-x)2=25,解得x=3或4,
②当MN为最大线段时,依题意MN2=AM2+NB2,
即(7-x)2=x2+25,解得x=$\frac{12}{7}$,
③当BN为最大线段时,依题意BN2=AM2+MN2.
即x2=25+(7-x)2,解得x=$\frac{37}{7}$,
综上所述BN的长为3或4或$\frac{12}{7}$或$\frac{37}{7}$.
(3)如图2中,把△CBQ绕点C顺时针旋转90°,得△ACR,连结RP.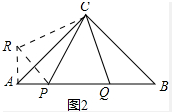
则∠CAR=∠CBQ=45°,
∴∠RAP=90°,
∴AP2+AR2=PR2,
∵AR=BQ,
∴AP2+BQ2=PR2,
∵P、Q是AB的勾股分割点,
∴AP2+BQ2=PQ2,
∴PR=PQ,
在△PCR和△PCQ中,
$\left\{\begin{array}{l}{CR=CQ}\\{PR=PQ}\\{PC=PC}\end{array}\right.$,
∴△PCR≌△PCQ,
∴∠PCQ=∠PCR,
∵∠PCQ+∠PCR=90°,
∴∠PCQ=45°.
点评 本题参考三角形综合题、勾股定理的逆定理、全等三角形的判定和性质等知识,解题的关键是理解题意,学会分类讨论,注意不能漏解,学会利用旋转添加辅助线构造全等三角形,属于中考常考题型.

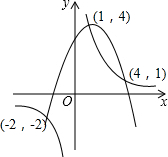 二次函数y=ax2+bx+c(a≠0)的图象与反比例函数y=$\frac{k}{x}$(k≠0)的图象相交(如图),则不等式ax2+bx+c>$\frac{k}{x}$的解集是( )
二次函数y=ax2+bx+c(a≠0)的图象与反比例函数y=$\frac{k}{x}$(k≠0)的图象相交(如图),则不等式ax2+bx+c>$\frac{k}{x}$的解集是( )| A. | 1<x<4或x<-2 | B. | 1<x<4或-2<x<0 | ||
| C. | 0<x<1或x>4或-2<x<0 | D. | -2<x<1或x>-4 |
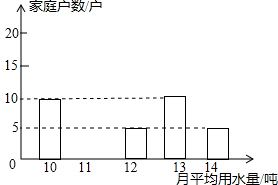 为了倡导“节约用水,从我做起”,南沙区政府决定对区直属机关300户家庭的用水情况作一次调查,区政府调查小组随机抽查了其中50户家庭一年的月平均用水量(单位:吨),调查中发现每户用水量均在10-14吨/月范围,并将调查结果制成了如图所示的条形统计图.
为了倡导“节约用水,从我做起”,南沙区政府决定对区直属机关300户家庭的用水情况作一次调查,区政府调查小组随机抽查了其中50户家庭一年的月平均用水量(单位:吨),调查中发现每户用水量均在10-14吨/月范围,并将调查结果制成了如图所示的条形统计图.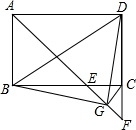 如图,在矩形ABCD中,∠BAD的平分线交BC于点E,交DC的延长线于点F,取EF的中点G,连接CG,BG,BD,DG,下列结论:
如图,在矩形ABCD中,∠BAD的平分线交BC于点E,交DC的延长线于点F,取EF的中点G,连接CG,BG,BD,DG,下列结论:
 在如图所示的直角坐标系中,解答下列问题:
在如图所示的直角坐标系中,解答下列问题: 如图,平行四边形ABCD中,∠B=60°,AB=8cm,AD=10cm,点P在边BC上从B向C运动,点Q在边DA上从D向A运动,如果P,Q运动的速度都为每秒1cm,那么当运动时间t=7秒时,四边形ABPQ是直角梯形.
如图,平行四边形ABCD中,∠B=60°,AB=8cm,AD=10cm,点P在边BC上从B向C运动,点Q在边DA上从D向A运动,如果P,Q运动的速度都为每秒1cm,那么当运动时间t=7秒时,四边形ABPQ是直角梯形.