Question

1．在如图所示的直角坐标系中，解答下列问题：
（1）分别写出点A、B的坐标；
（2）将△ABC绕点A顺时针旋转90°，画出旋转后的△AB₁C₁；
（3）求线段BB₁所在直线的解析式．

Answer 1

分析 （1）利用坐标的表示方法写出A、B点的坐标；
（2）利用网格特点和旋转的性质画出点B、C的对应点B₁、C₁，从而得到△AB₁C₁；
（3）先写出B₁点的坐标，然后利用待定系数法求解．

解答 解：（1）点A、B的坐标分别为（2，0），（-1，-4）；
（2）如图，△AB₁C₁为所作；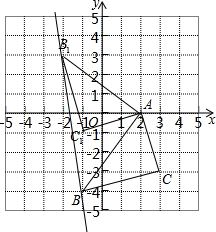

（3）B₁点的坐标为（-2，3），
设直线BB₁的解析式为y=kx+b，
把B（-1，-4），B₁（-2，3）代入得$\left\{\begin{array}{l}{-k+b=-4}\\{-2k+b=3}\end{array}\right.$，解得$\left\{\begin{array}{l}{k=-7}\\{b=-11}\end{array}\right.$，
所以直线BB₁的解析式为y=-7x+11．

点评 本题考查了作图-旋转变换：根据旋转的性质可知，对应角都相等都等于旋转角，对应线段也相等，由此可以通过作相等的角，在角的边上截取相等的线段的方法，找到对应点，顺次连接得出旋转后的图形．也考查了待定系数法求一次函数解析式．