题目内容
已知a2+3a+1=0,求:①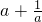 ,②
,②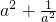 ,③
,③ .
.
解:①∵a2+3a+1=0,
∴a≠0,
∴在等式的两边同时除以a,得
a+3+ =0,
=0,
∴a+ =-3;
=-3;
②由①知,a+ =-3,则(a+
=-3,则(a+ )2=
)2=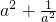 +2=9,
+2=9,
解得,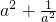 =7;
=7;
③由②知,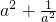 =7,则(
=7,则(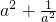 )2=
)2= +2=49,
+2=49,
解得, =47.
=47.
分析:①在等式是两边同时除以不等于零的a来求代数式的值;
②通过求①的代数式的平方来求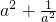 的值;
的值;
③通过求②的代数式的平方来求 的值.
的值.
点评:本题考查了完全平方公式.找出①、②、③三个代数式间的关系是解题的关键.
∴a≠0,
∴在等式的两边同时除以a,得
a+3+
 =0,
=0,∴a+
 =-3;
=-3;②由①知,a+
 =-3,则(a+
=-3,则(a+ )2=
)2=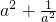 +2=9,
+2=9,解得,
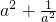 =7;
=7;③由②知,
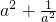 =7,则(
=7,则(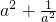 )2=
)2= +2=49,
+2=49,解得,
 =47.
=47.分析:①在等式是两边同时除以不等于零的a来求代数式的值;
②通过求①的代数式的平方来求
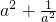 的值;
的值;③通过求②的代数式的平方来求
 的值.
的值.点评:本题考查了完全平方公式.找出①、②、③三个代数式间的关系是解题的关键.

练习册系列答案
相关题目