题目内容
如图,在 △
△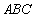 中,点
中,点 、
、 分别为边
分别为边 、
、 上的点,且
上的点,且 ∥
∥ ,若
,若 ,
, ,
, ,则
,则 的长为( )
的长为( )
 A.3 B.6 C.9 D.12
A.3 B.6 C.9 D.12

B

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
题目内容
如图,在 △
△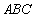 中,点
中,点 、
、 分别为边
分别为边 、
、 上的点,且
上的点,且 ∥
∥ ,若
,若 ,
, ,
, ,则
,则 的长为( )
的长为( )
 A.3 B.6 C.9 D.12
A.3 B.6 C.9 D.12

B

 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案