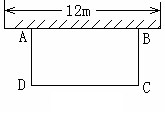
题目内容
已知:二次函数 (m为常数).
(m为常数).
(1)若这个二次函数的图象与x轴只有一个公共点A,且A点在x轴的正半轴上.
①求m的值;
②四边形AOBC是正方形,且点B在y轴的负半轴上,现将这个二次函数的图象平移,使平移后的函数图象恰好经过B,C两点,求平移后的图象对应的函数解析式;
(2) 当0≤ ≤2时,求函数
≤2时,求函数 的最小值(用含m的代数式表示).
的最小值(用含m的代数式表示).

解:(1)①∵ 二次函数 的图象与x轴只有一个公共点A,
的图象与x轴只有一个公共点A,
∴ 
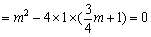 .
.
整理,得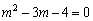 .
.
解得,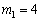 ,
,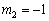 .
.
又点A在x轴的正半轴上,
∴ 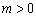 .
.
∴ m=4.
②由①得点A的坐标为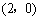 .
.
∵ 四边形AOBC是正方形,点B在y轴的负半轴上,
∴ 点B的坐标为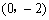 ,点C的坐标为
,点C的坐标为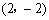 .
.
设平移后的图象对应的函数解析式为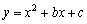 (b,c为常数).
(b,c为常数).
∴ 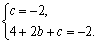
解得
∴平移后的图象对应的函数解析式为 .
.
(2)函数 的图象是顶点为
的图象是顶点为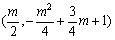 ,且开口向上的抛物线.分三种情况:
,且开口向上的抛物线.分三种情况:
(ⅰ)当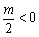 ,即
,即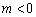 时,函数在0≤
时,函数在0≤ ≤2内y随x的增大而增大,此时函数的最小值为
≤2内y随x的增大而增大,此时函数的最小值为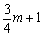 ;
;
(ⅱ)当0≤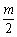 ≤2,即0≤
≤2,即0≤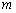 ≤4时,函数的最小值为
≤4时,函数的最小值为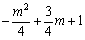 ;
;
(ⅲ)当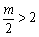 ,即
,即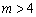 时,函数在0≤
时,函数在0≤ ≤2内y随x的增大而减小,此时函数的最小值为
≤2内y随x的增大而减小,此时函数的最小值为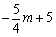 .
.
综上,当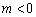 时,函数
时,函数 的最小值为
的最小值为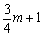 ;
;
当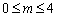 时,函数
时,函数 的最小值为
的最小值为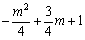 ;
;
当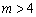 时,函数
时,函数 的最小值为
的最小值为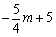 .
.

练习册系列答案
相关题目
 △
△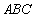 中,点
中,点 、
、 分别为边
分别为边 、
、 上的点,且
上的点,且 ∥
∥ ,若
,若 ,
, ,
, ,则
,则 的长为( )
的长为( )  A.3 B.6 C.9 D.12
A.3 B.6 C.9 D.12
 .求:BC的长.
.求:BC的长.
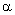 角后得到△A′B′C,当点A的对应点A' 落在AB边上时,旋转角
角后得到△A′B′C,当点A的对应点A' 落在AB边上时,旋转角
 .
. 
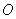 的半径为4 cm,如果圆心
的半径为4 cm,如果圆心 ,则它们的周长比是_______.
,则它们的周长比是_______. 中,DE∥BC,且AD:AB=2:3,则DE:BC的值为
中,DE∥BC,且AD:AB=2:3,则DE:BC的值为 B.
B. C.
C. D.2
D.2 
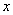 m,DC的长为
m,DC的长为 m.
m.