题目内容
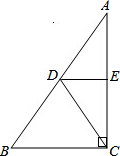如图，在△ABC中，∠ACB=90°，点D是斜边AB的中点，AE=CE，求证：∠CDE=∠B．考点：直角三角形斜边上的中线,等腰三角形的判定与性质
专题：证明题
分析：根据直角三角形斜边上的中线等于斜边的一半可得CD=AD，再根据等腰三角形三线合一的性质可得∠CDE=∠ADE，DE⊥AC，然后求出根据两直线平行，同位角相等证明即可．
解答：证明：∵∠ACB=90°，点D是斜边AB的中点，
∴CD=AD=
AB，
∵AE=CE，
∴∠CDE=∠ADE，DE⊥AC，
∴DE∥BC，
∴∠B=∠ADE，
∴∠CDE=∠B．
∴CD=AD=
| 1 |
| 2 |
∵AE=CE，
∴∠CDE=∠ADE，DE⊥AC，
∴DE∥BC，
∴∠B=∠ADE，
∴∠CDE=∠B．
点评：本题考查了直角三角形斜边上的中线等于斜边的一半的性质，等腰三角形的判定与性质，熟记各性质是解题的关键．
练习册系列答案
相关题目
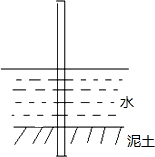一根竹竿插入一水池底部的淤泥中（如图），竹竿的入泥部分占全长的