题目内容
2.如图,一架2.5米长的梯子AB,斜靠在一竖直的墙ON上,这时梯足B到墙底端O的距离为0.7米,如果梯子的顶端沿墙下滑0.4米,那么梯足将向外移多少米?
分析 在直角△ABO中,已知AB,BO可以求AO,在△COD中,再利用勾股定理计算出DO的长,进而可得BD的长.
解答 解:在直角△ABO中,AB为斜边,已知AB=2.5米,BO=0.7米,
则根据勾股定理求得AC=$\sqrt{A{B}^{2}-B{O}^{2}}$=2.4米,
∵A点下移0.4米,
∴CO=2米,
在Rt△COD中,已知CD=2.5米,CO=2米,
则根据勾股定理DO=$\sqrt{C{D}^{2}-C{O}^{2}}$=1.5米,
∴BD=OD-BO=1.5米-0.7米=0.8米,
所以梯子向外平移0.8米.
点评 本题考查了勾股定理在实际生活中的应用,考查了勾股定理的灵活运用,本题中找到AB=CD的等量关系是解题的关键.

练习册系列答案
相关题目
12.下列不是二元一次方程组的是( )
| A. | $\left\{\begin{array}{l}2x+9y=0\\ x+y=0\end{array}\right.$ | B. | 3x=4y=1 | C. | $\left\{\begin{array}{l}\frac{1}{x}-2y=2\\ x=1\end{array}\right.$ | D. | $\left\{\begin{array}{l}x=3\\ y=2\end{array}\right.$ |
13.手机给我们带来方便的同时也给我们带来辐射,手机在刚拨出号码时对人体的辐射最大,其实在我们身处的自然环境中,每人一年接受的宇宙射线及天然辐射照射量约为3100微西弗(1西弗等于1000毫西弗,1毫西弗等于1000微西弗),用科学记数法可表示为( )
| A. | 3.1×106西弗 | B. | 3.1×103西弗 | C. | 3.1×10-3西弗 | D. | 3.1×10-6西弗 |
10.直角三角形两条直角边长分别是1cm,$2\sqrt{2}$cm.那么斜边的长是( )
| A. | 3cm | B. | $3\sqrt{2}$cm | C. | $2\sqrt{3}$cm | D. | 5cm |
17. 如图所示,矩形ABCD中,AB=4,BC=$4\sqrt{3}$,点E是折线ADC上的一个动点(点E与点A不重合),点P是点A关于BE的对称点.在点E运动的过程中,使△PCB为等腰三角形的点E的位置共有( )
如图所示,矩形ABCD中,AB=4,BC=$4\sqrt{3}$,点E是折线ADC上的一个动点(点E与点A不重合),点P是点A关于BE的对称点.在点E运动的过程中,使△PCB为等腰三角形的点E的位置共有( )
 如图所示,矩形ABCD中,AB=4,BC=$4\sqrt{3}$,点E是折线ADC上的一个动点(点E与点A不重合),点P是点A关于BE的对称点.在点E运动的过程中,使△PCB为等腰三角形的点E的位置共有( )
如图所示,矩形ABCD中,AB=4,BC=$4\sqrt{3}$,点E是折线ADC上的一个动点(点E与点A不重合),点P是点A关于BE的对称点.在点E运动的过程中,使△PCB为等腰三角形的点E的位置共有( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
7.如果17m长的梯子的底端距离建筑物8m,那么梯子可达到该建筑物的高度大约是( )NN#
| A. | 13m | B. | 14m | C. | 15m | D. | 16m |
11.某样本容量是60,分组后,第2组的频率是0.15,那么第2组的频数是( )
| A. | 9 | B. | 18 | C. | 60 | D. | 400 |
12.下列二次根式有意义的范围为x>2的是( )
| A. | y=$\sqrt{x-2}$ | B. | y=$\frac{1}{\sqrt{2x-1}}$ | C. | y=$\frac{1}{\sqrt{x-2}}$ | D. | y=$\sqrt{2x-1}$ |
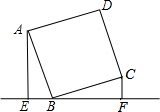 如图,直线L过正方形ABCD的顶点B,点A、点C到直线L的距离分别是2和1,求正方形ABCD的边长?
如图,直线L过正方形ABCD的顶点B,点A、点C到直线L的距离分别是2和1,求正方形ABCD的边长?