Question

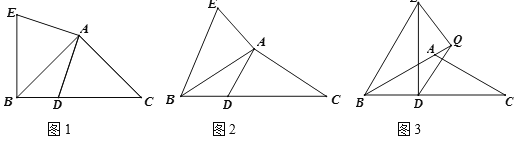
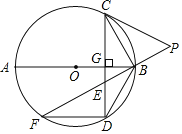
【题目】如图，在Rt△ABC中，∠C＝90°，AC＝4cm，BC＝5cm，点D在BC上，且CD＝3cm．动点P，Q同时从点C出发，均以1cm/s的速度运动，其中点P沿CA向终点A运动；点Q沿CB向终点B运动．过点P作PE∥BC，分别交AD，AB于点E，F，设动点Q运动的时间为t秒．

（1）求DQ的长（用含t的代数式表示）；

（2）以点Q，D，F，E为顶点围成的图形面积为S，求S与t之间的函数关系式；

（3）连接PQ，若点M为PQ中点，在整个运动过程中，直接写出点M运动的路径长．

Answer 1

【答案】（1）当0≤t≤3时，DQ＝3﹣t；当3＜t≤5时，DQ＝t﹣3．

（2）；

（3）3.

【解析】

（1）由于CD=3cm，运动速度为1m/s，故进行分类讨论，分别为当0≤t≤3时，当3＜t≤5时，分别计算出DQ的长度即可.

（2）根据梯形面积公式和三角形面积公式，分类进行讨论，分别当0≤t≤3时和当3＜t≤4时，四点围成的是一个梯形，当4＜t≤5时，E、F点重合，此时围成的是一个三角形.分别计算，用含t的式子将S表示出来即可.

（3）根据题意，CB＞CA，故M点的运动轨迹分为两段，一段为P点运行到A点，Q点运行到与CA的长相等的地方可设为J点，此时M运行的路经长为等腰直角△JCA的底边的垂线CR，第二段,过R点作BC的平行线，与AB交于点T,此时P点已经停止在了A点，Q点继续由J点向B点运动，此时M点的运行轨迹即为RT的长，分别计算出两段的长，相加即可.

解：（1）当0≤t≤3时，DQ＝CD-CQ

∵CD=3,CQ=t,

∴DQ =3﹣t；

当3＜t≤5时，DQ＝CQ-CD

∵CQ =t，CD =3，

∴DQ =t﹣3．

（2）①当0≤t≤3时，如图，

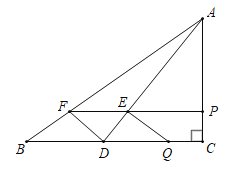
∵PC＝t，AC＝4，

∴，

，

，

∴．

②当3＜t≤4时，如图，

∴．

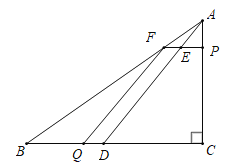
③当4＜t≤5时，如图，

∴．

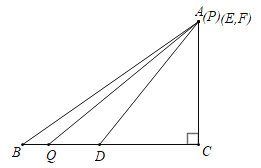
综上所述

（3）点M运动的路径长为2，

如图，在CB上取一点J，使得CJ＝CA，连接AJ，作CR⊥AJ于R，RT∥BC交AB于T．

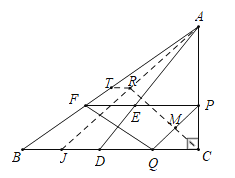
由题意点M的运动路径是C→R→T，

∵CA＝CJ＝4，CR⊥AJ，∠ACJ＝90°，

∴AJ＝4，AR＝RJ，

∴CR＝AJ＝2，

∵RT∥BJ，AR＝RJ，

∴AT＝TB，

∴RT＝BJ＝，

∴点M的运动路径的长为2．